
Question and Answers Forum
IntegrationQuestion and Answers: Page 93
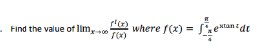
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 93 |
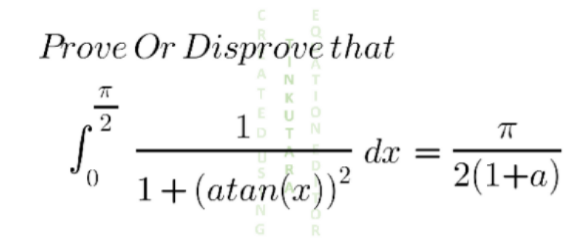
|
| 𝛗=∫_0 ^( 1) ((ln(x^2 +1))/x^2 )dx f(a)=∫_0 ^( 1) ((log(ax^2 +1))/x^2 )dx f ′(a)=∫_0 ^( 1) (x^2 /((ax^2 +1)x^2 ))dx=(1/a)∫_0 ^( 1) (dx/(x^2 +((1/( (√a))))^2 )) =((√a)/a)[tan^(−1) (x(√a) )]_0 ^1 =((√a)/a)tan^(−1) ((√a)) f(a)=^((√a) =u) ∫2tan^(−1) (u)du =2{u.tan^(−1) (u)−∫(u/(1+u^2 ))du}+C =2(√a) tan^(−1) ((√a) )−ln(1+a)+C f(0)=0=0+C⇒C=0 f(1)=𝛗=2((π/4))−ln(2)=(π/2)−ln(2) |
| ..........nice calculus......... suppose that::: ϕ(p)=∫_0 ^( ∞) ((ln(1+x))/((p+x)^2 )) ...✓ find the value of:: ∫^( 1) _0 ((ϕ(p))/(1+p))dp=?... |
| ....advanced calculus.... 𝛗=∫_0 ^( (π/2)) x.(tan(x))^(1/2) dx=?? |
| ......nice calculus..... prove:: ∫_0 ^( 1) (1/(1+ln^2 (x)))dx=∫_(0 ) ^( ∞) ((sin(x))/(1+x))dx |
| f(x)=∫_(−Π/4) ^(Π∫/4) e^(xtant) dt |
| ∫_0 ^((50π)/3) ∣sinx∣dx |
| (a) Let I(α)=∫_0 ^∞ e^(−(x−(α/x))^2 ) dx Show that it is legitimate to take the derivative of I(α) and also I′(α)= 0. Then show that I(α)=((√π)/2). (b) Use (a) to prove ∫_0 ^∞ e^(−(x^2 +α^2 x^(−2) )) dx=((√π)/2)e^(−2α) . |
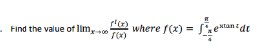
|
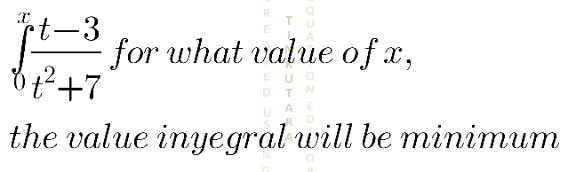
|
| ∫ (dx/(sin^6 x)) ? |
| If α>0 and β>0, prove ∫_0 ^∞ ((ln(αx))/(β^2 +x^2 ))dx=(π/(2β))ln(αβ) |
| calculate A_λ =∫_0 ^∞ ((cos^4 x)/((x^2 +λ^2 )^2 ))dx 2) find the value of ∫_0 ^∞ ((cos^4 x)/((x^2 +3)^2 ))dx |
| if f(x)=x^3 −3x+2 determine f^(−1) (x) and ∫ f^(−1) (nf(x))dx with n integr |
| find ∫ ((arctan(2x))/(x+3))dx |
| find U_n =∫_(1/n) ^n (1−(1/x^2 ))arctan(x+(1/x))dx and lim_(n→∞) U_n |
| find ∫_0 ^∞ ((arctan(x^2 ))/(x^4 +1))dx |
| calculate ∫∫_([0,1]^2 ) e^(−(x^2 +y^2 )) arctan(x^2 +y^2 )dxdy |
| calculate ∫ (dx/(x^n (√(x^2 −1)))) |
| find ∫_0 ^1 (x^a /(1−x))dx |
| ......sdvanced cslculus...... if x∈R^+ and:: 𝛗(x)=∫_0 ^( x) ((e^t −1)/t)ln((x/t))dt then prove that :: Ψ=∫_0 ^( ∞) e^(−x) 𝛗(x)dx=ζ(2) |
| ∫ (dx/(sin x (√(cos x)))) =? |
| lim_(x→0) (x^(2021) /(x−ln(Σ_(k=0) ^(2020) (x^k /(k!))))) =^? 2021! |
| calculate ∫_0 ^∞ (t^a /(1+t+t^2 ))dt study first the convergence (a real) |
| please a generall Form for C(n) C(n)=(4/π^2 )Σ_(k=1) ^n (−1)^(k−1) ζ(2k)ζ(2n−2k) |
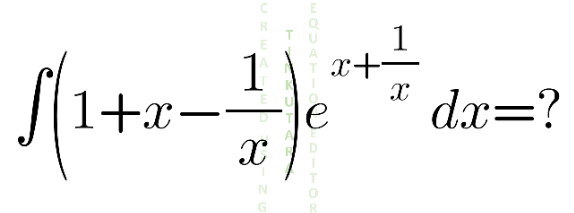
|