
Question and Answers Forum
IntegrationQuestion and Answers: Page 94



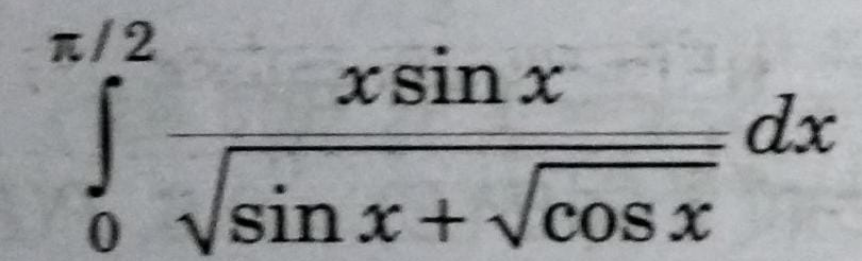


|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 94 |
| find the area between the curve y = 3 + 2x −x^2 , the x−axis and the line y = 3. find the volume of the solid generated when the curve is rotated completely about the line y = 3 |
| Λ = ∫ x^3 (x^3 +1)^(10) dx |
| ...advanced calculus.... evaluate:: 𝛗=Im(∫_0 ^( (π/2)) li_2 (sin(x))+li_2 (csc(x))dx) |
| calculate ∫_0 ^∞ ((logx)/(x^4 +x^2 +1))dx |
| calculate ∫_(−∞) ^(+∞) ((cos(2x)dx)/(x^4 +x^2 +1)) |
| calculate ∫_0 ^∞ e^(−z^2 ) dz with z complex |

|
| 1) find ∫ (dx/((x+1)^2 (x−3)^4 )) 2) deduce the decomposition of F(x)=(1/((x+1)^2 (x−3)^4 )) |
| Evaluate (1) ∫_0 ^1 ∫_0 ^x ∫_0 ^y (3x^2 +2y^2 −3z^2 )dxdydz (2) ∫(2x−2)^3 dx (3) ∫(((x−5)/(x^2 −10x+2)))dx |

|
| Evaluate ∮_c ydy where c is a circle x^2 +y^2 =4 |
| sin^2 (4x)+cos^2 (x)=2sin (4x)cos^2 (x) |
| Let f(x)=∫_0 ^x e^(−t^2 ) dt , Prove ∫_0 ^∞ e^(−x^2 +f(x)) dx=e^((√π)/2) −1. |
| Given { ((f(3)=4 , f ′(3)=−2)),((f(8)=5 , f ′(8)=3)) :} find ∫_3 ^( 8) x f ′′(x) dx . |

|
| let U_n =∫_(−∞) ^(+∞) ((cos(nx))/((x^2 −x+1)^2 ))dx calculate lim_(n→+∞) e^n^2 U_n |
| ∫_(−2π) ^(4π) (3/(5−4cosx))dx |
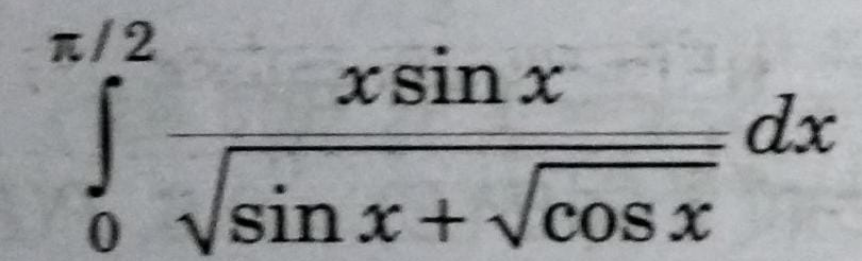
|
| Ω = ∫ ((x−1)/((x−2)(x^2 −2x+2)^2 )) dx |
| ∫ ((x^2 +1)/(x^4 +x^2 +1)) dx |
| ∫(x+(1/2))ln(1+(1/x))−x dx=...? |
| ∫(1/(x^(1/3) +1))dx=...? |

|
| ... nice ................. calculus ... evaluation::::: 𝛗=^(???) ∫_0 ^( (π/2)) sin(x)ln(sin(x))dx solution::::: 𝛗=^(⟨cos(x)=y⟩) (1/2)∫_0 ^( 1) ln(1−y^2 )dy =−(1/2)∫_0 ^( 1) Σ_(n=1 ) ^∞ (y^(2n) /n)=((−1)/2)Σ_(n=1) ^∞ ((1/n)∫_0 ^( 1) y^(2n) dy) =((−1)/2)Σ_(n=1) ^∞ (1/(n(2n+1)))=−Σ_(n=1) ^∞ (1/(2n)) −(1/(2n+1)) =−((1/2)−(1/3)+(1/4)−(1/5)+...) =−1+(1−(1/2)+(1/3)−...) =−1+Σ_(n=1) ^∞ (((−1)^(n−1) )/n)=_(harmonic seties) ^(alternating) −1+ln(2) ∴ 𝛗= −1+ln(2)=ln((2/e)) |

|
| .... Advanced ...... Calculus.... prove that : determinant (((i :: Π_(n=0) ^∞ (1−(x^2 /((2n+1)^2 ))) =cos(((πx)/2)) ✓ )),((ii :: Π_(n=0) ^∞ (1+(x^2 /((2n+1)^2 )))= cosh(((πx)/2)) ✓✓))) ............. |