
Question and Answers Forum
IntegrationQuestion and Answers: Page 95
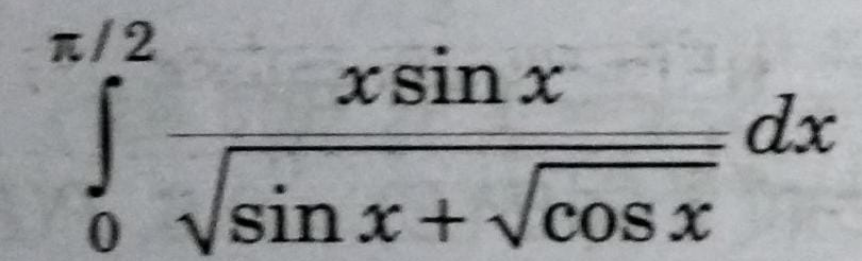



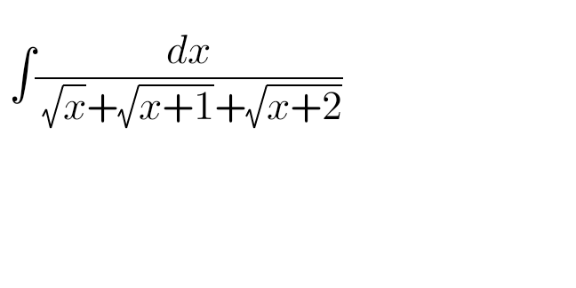

|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 95 |
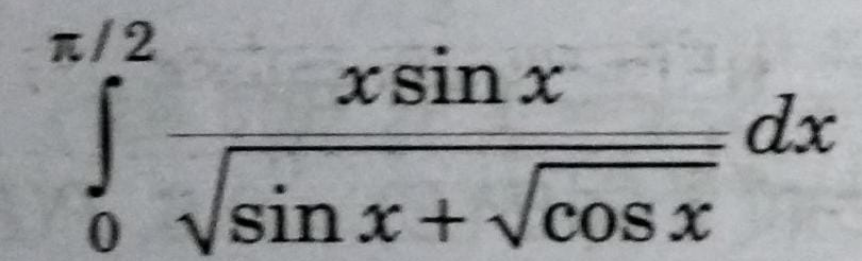
|
| Ω = ∫ ((x−1)/((x−2)(x^2 −2x+2)^2 )) dx |
| ∫ ((x^2 +1)/(x^4 +x^2 +1)) dx |
| ∫(x+(1/2))ln(1+(1/x))−x dx=...? |
| ∫(1/(x^(1/3) +1))dx=...? |

|
| ... nice ................. calculus ... evaluation::::: 𝛗=^(???) ∫_0 ^( (π/2)) sin(x)ln(sin(x))dx solution::::: 𝛗=^(⟨cos(x)=y⟩) (1/2)∫_0 ^( 1) ln(1−y^2 )dy =−(1/2)∫_0 ^( 1) Σ_(n=1 ) ^∞ (y^(2n) /n)=((−1)/2)Σ_(n=1) ^∞ ((1/n)∫_0 ^( 1) y^(2n) dy) =((−1)/2)Σ_(n=1) ^∞ (1/(n(2n+1)))=−Σ_(n=1) ^∞ (1/(2n)) −(1/(2n+1)) =−((1/2)−(1/3)+(1/4)−(1/5)+...) =−1+(1−(1/2)+(1/3)−...) =−1+Σ_(n=1) ^∞ (((−1)^(n−1) )/n)=_(harmonic seties) ^(alternating) −1+ln(2) ∴ 𝛗= −1+ln(2)=ln((2/e)) |

|
| .... Advanced ...... Calculus.... prove that : determinant (((i :: Π_(n=0) ^∞ (1−(x^2 /((2n+1)^2 ))) =cos(((πx)/2)) ✓ )),((ii :: Π_(n=0) ^∞ (1+(x^2 /((2n+1)^2 )))= cosh(((πx)/2)) ✓✓))) ............. |

|
| .... nice ................ calculus... evaluation of :: 𝛗=∫_0 ^( ∞) xe^(−x) (√(1−e^(−x) )) dx solution:: 1−e^(−x) =t ⇒ {_( x=−ln(1−t)) ^( e^(−x) dx=dt) 𝛗=−∫_0 ^( 1) ln(1−t).t^(1/2) dt =∫_0 ^( 1) Σ_(n=1) ^∞ (t^(n+(1/2)) /n)dt=Σ_(n=1) ^∞ (1/(n(n+(3/2)))) .... ∴ 𝛗= Σ_(n=1) ^∞ (1/(n(n+(3/2))))=Σ_(n=1) ^∞ (1/n)−(1/(n+(3/2))) .... =(2/3){γ−γ+Σ_(n=1) ^∞ ((1/n)−(1/(n+(3/2))))} .... we know that : ψ(s+1) := −γ+Σ_(n=1) ^∞ ((1/n)−(1/(n+s))) ..... ∴ 𝛗=(2/3)(γ+ψ((5/2))) .... on the oyher hand we have:: ψ(s+1)=(1/s)+ψ(s) ...... ψ((1/2))=−γ−2ln(2) ...... ψ((5/2))=(2/3)+ψ((3/2))=(2/3)+(2+ψ((1/2))) =(2/3)+2+(−γ−2ln(2)) .... ∴ ψ((3/2))=(8/3)−γ−ln(4) .... :::::: 𝛗 =(2/3)(γ+(8/3)−γ−ln(4)) .... 𝛗=(2/3)((8/3)−ln(4))=(4/3)((4/3)−ln(2)) .... ...... 𝛗= (4/3)((4/3)−ln(2))......✓✓ .... ... prepare by mr rizzy−aka... solution with detais :m.n.july.1970 |
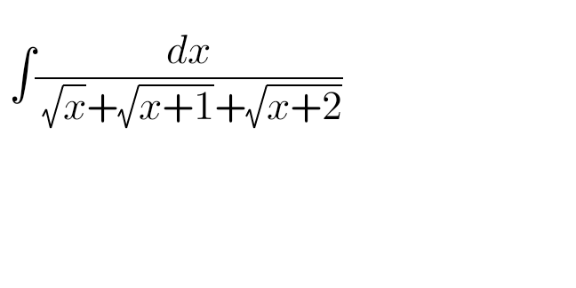
|
| hi, guyz ! let′s try this : I=∫_0 ^( 1) ((sin^2 x)/(cos^3 x))dx. |

|
| let U_n =∫_(−∞) ^∞ ((cos(nx))/((x^2 −x+1)^2 ))dx calculate lim_(n→∞) e^n^2 U_n |
| find ∫_0 ^1 x^n ln(1−x^4 )dx with n integr natural |
| calculate ∫_0 ^∞ (dx/(((√x)+(√(1+x^2 )))^3 )) |
| calculate ∫_0 ^(+∞) ((xarctan(2x))/((x^2 +1)^2 ))dx |
| f(x)=3x^2 +6x,[−1,5] find−the−average−value |
| ∫(x^2 +3x)cos (x)dx |
| ∫t^7 ln(t)dt |
| .....calculus preliminary.... Q: f(x)=2^x −2^(−x) ⇒ f^( −1) (x)=??? solution: y=2^x −2^(−x) ..... y=((2^(2x) −1)/2^x ) ⇒2^(2x) −y2^x −1=0 (∗) ... :: 2^x =t⇒ t>0 ...✓ .... (∗)→... t^2 −ty−1=0 .... Δ=y^2 +4>0...✓ ... t=((y+(√(y^2 +4)))/2) ...... :: 2^x =((y+(√(y^2 +4)))/2) ⇒_(both sides) ^(taking log) .... x:=log_2 (((y+(√(y^2 +4)))/2)) f^( −1) (x)=log_2 (((x+(√(x^2 +4)))/2)) ✓✓ ......................... |
| Z = ∫_0 ^( π/2) arctan (sin x) dx + ∫_0 ^( π/4) arcsin (tan x) dx |
| ∫(√((x^2 +x)^3 )) dx help me |
| f(x)=1+Σ_(n=2) ^∞ (((−x)^n )/n) |
| Let f(0) = a ; f(3)=0 and f ′(x)=e^x^4 what is the value ∫_0 ^( 3) x^2 f(x) dx ? |