
Question and Answers Forum
IntegrationQuestion and Answers: Page 98






Pg 93 Pg 94 Pg 95 Pg 96 Pg 97 Pg 98 Pg 99 Pg 100 Pg 101 Pg 102
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 98 |
| ∫_0 ^1 ((x^4 (1−x)^4 )/(1+x^2 )) dx =? |
| ∫^( (π/2)) _0 (dx/(1+tan^(2014) (x))) = ((πe^q )/p) Find 2p−q. |
| ∫_0 ^2 x^5 (8−x^3 )^(1/3) dx |
| ∫_0 ^(π/2) (tan(x))^(1/n) dx ... |
| If ∫ ((tan x)/(1+tan x+tan^2 x)) dx = x−(k/( (√A))) tan^(−1) (((k tan x+1)/( (√A))))+C where C is constant of integration. then the ordered pair (k,A) is equal to |

|
| ....mathematical analysis... prove that:: 𝛗=∫_0 ^( ∞) ((sin^3 (x))/x^3 )dx=((3π)/8) ∗∗∗∗.......... |

|
| (∫_0 ^(π/2) (√(sin(x)))dx)^2 +(∫_0 ^(π/2) (√(cos(x)))dx)^2 <8((√2)−1) |
| ∫_(−π/2) ^(3π/2) (sin^(−1) (∣sin x∣)+cos^(−1) (∣cos x∣)) dx |
| .... nice calculus... prove that : 𝛗=∫_0 ^( ∞) ((sin(x).log^2 (x))/x) =(π/(24))(12γ^( 2) +π^2 ) ..... |

|
| ∫(x−1)^(x+1) dx |

|
| ∫_0 ^(π/2) ((√(sin (x)))+(√(cos (x))))dx |

|
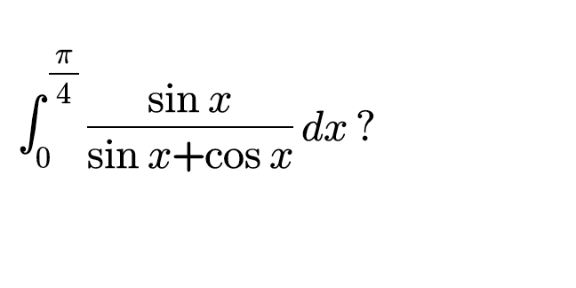
|
| ∫_0 ^∞ ((log x)/(1+x^2 +x^4 )) dx=...? |
| ....advanced calculus... evaluate : 𝛗=∫_0 ^( ∞) xe^(−2x) ln(x)dx=??? |
| ∫_(−∞) ^∞ ((x^2 cos (px+q))/(x^2 +(p+q)^2 ))dx |
| I=∫ (dx/(x(x^2 +1)^3 )) |
| Ω=∫ ((sin^2 (x))/(1+sin^2 (x))) dx |

|
| Find the voloume bounded by z=(√(x^2 +y^2 )) and the plane y+z=3 |
| ∫_0 ^(π/2) (dx/(1+sin x)) →diverges or converges? |
| .... nice calculus.... prove that :: Σ_(n=1) ^∞ (((−1)^n ln(n))/n)=γln(2)−(1/2)ln^2 (2) |
Pg 93 Pg 94 Pg 95 Pg 96 Pg 97 Pg 98 Pg 99 Pg 100 Pg 101 Pg 102 |