
Question and Answers Forum
IntegrationQuestion and Answers: Page 99




Pg 94 Pg 95 Pg 96 Pg 97 Pg 98 Pg 99 Pg 100 Pg 101 Pg 102 Pg 103
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 99 |

|
| ... math analysis... φ= ∫_(−∞) ^( +∞) ((xsin(x))/(x^2 +2x+2))dx=? φ=∫_(−∞) ^( +∞) ((xsin(x))/((x+1)^2 +1))dx =^(x+1=t) ∫_(−∞) ^( +∞) (((t−1)sin(t−1))/(t^2 +1))dt =∫_(−∞) ^( +∞) ((tsin(t)cos(1)−tcos(t)sin(1)−sin(t)cos(1)+cos(t)sin(1))/(t^2 +1))dt =2cos(1)∫_0 ^( ∞) ((tsin(t))/(t^2 +1))dt+2sin(1)∫_0 ^( ∞) ((cos(t))/(t^2 +1))dt =2cos(1).(π/(2e))+2sin(1).(π/(2e)) =(π/e)(cos(1)+sin(1)).... |
| ∫(sin^4 x.cos^4 x)dx |
| Evaluate ∫_(−∞) ^∞ ((sinx)/(x^2 +2x+2))dx |

|
| ∫ ((x!)/( (√x))) dx = ? |
| ...nice calculus.. Φ=∫_0 ^( ∞) ((ln(cosh(x)))/(cosh(x)))dx=??? |
| ... calculus ... φ =∫_0 ^( ∞) ((tanh^2 (x)dx)/x^2 ) =? |
| ...advanced calculus... Ω=∫_0 ^( ∞) (dx/(x^5 (e^(1/x) −1)))=? |
| ... analysis (II)... evaluate :: ∅=∫_1 ^( 10) x^2 d({x})=? {x} :: fractional part of x ... |
| ∗∗∗ calculus (I) ∗∗∗ please evaluate:: φ=∫(dx/(sin(2x)ln(tan(x)))) Trinity College Cambridge ....1897... |
| calculate ∫_(−∞) ^∞ ((cos(x^n ))/(1+x^n ))dx with n≥2 integr |
| f(x)= { ((−2x ; x≤0)),((f(x−1) ; x>0)) :} ∫_0 ^(100) f(x)dx =? |
| f(x)=2−x ∫_0 ^1 f(x)dx ⇒ ∫_0 ^1 f(x)dx=? |
| ∫_(C:∣z∣=1) ((−2i)/(Az^2 +2z+A))dz where C is a unit circle with radius 1 |
| advanced cslculus .. prove that: Σ_(n=0 ) ^∞ (1/(16^n ))((4/(8n+1))−(2/(8n+4))−(1/(8n+5))−(1/(8n+6)))=π |
| a curve C passes through (2,0) and the slope at (x,y) as (((x+1)^2 +(y−3))/(x+1)) Find the equation of the curve. |
| Nice calculus ∫_0 ^∞ ((x^(n−2) −1)/(x^n +1)) dx ? |
| Given y=f(x) satisfies (dy/dx) + ((√((x^2 −1)(y^2 −1)))/(xy)) = 1 lies at point (1,1) and ((√2) ,k). find k . |
| Nice integral ∫_0 ^( 1) ((sin (ln x))/(ln x)) dx =? |

|

|
| ...nice calculus... prove that : ∫_0 ^( 1) ln(Γ(x))cos(2πnx)dx=(1/(4n)) for example :∫_0 ^( 1) ln(Γ(x))cos(2πx)dx=(1/4) |
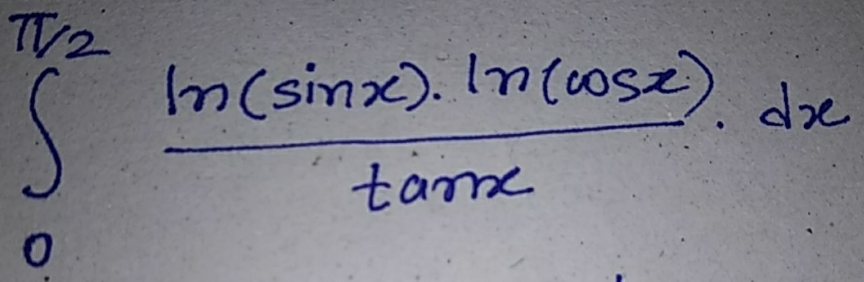
|
| ... nice calculus... evaluate :: Ω=∫_0 ^( ∞) ((sin(x))/x)ln(((a+cos^2 (x))/(b+cos^2 (x))))dx=? |
| ∫_0 ^1 (dx/( (√(1−x^4 )))) =? |
Pg 94 Pg 95 Pg 96 Pg 97 Pg 98 Pg 99 Pg 100 Pg 101 Pg 102 Pg 103 |