Question and Answers Forum
Question Number 20202 by Joel577 last updated on 24/Aug/17
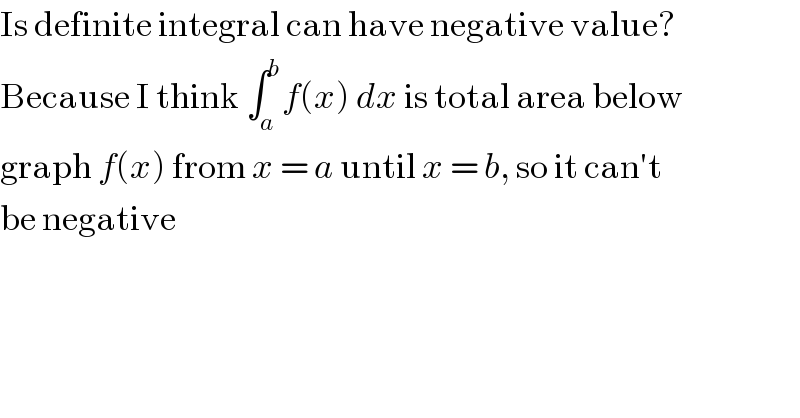
Commented by ajfour last updated on 24/Aug/17
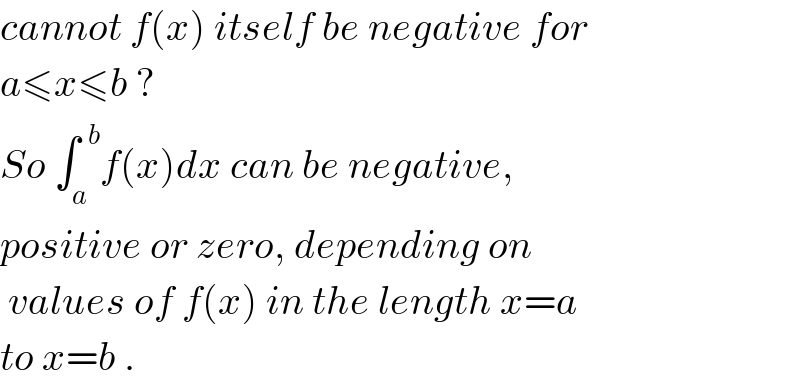
Commented by Joel577 last updated on 24/Aug/17

Commented by ajfour last updated on 24/Aug/17
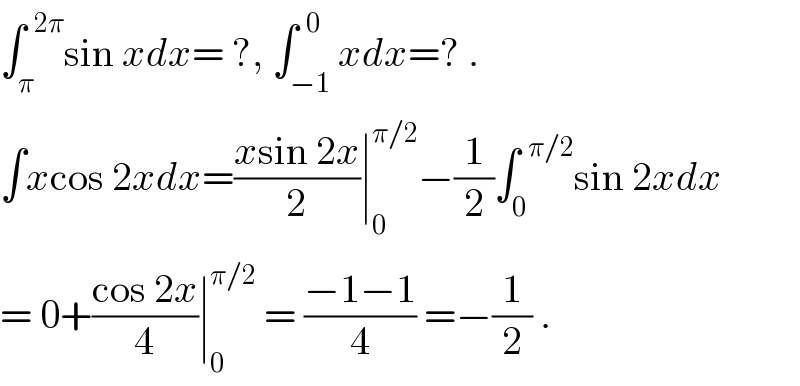
Commented by Joel577 last updated on 24/Aug/17
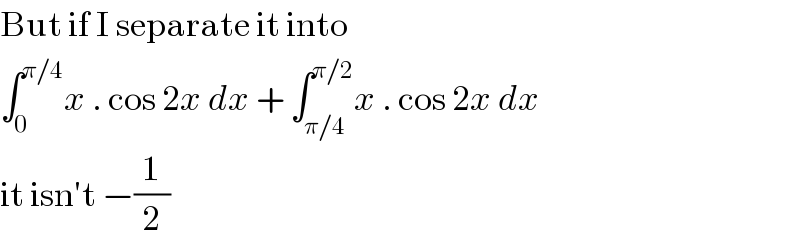
Commented by ajfour last updated on 24/Aug/17
![[((xsin 2x)/2)+((cos 2x)/4)]∣_0 ^(π/4) +[((xsin 2x)/2)+((cos 2x)/4)]∣_(π/4) ^(π/2) =((π/8)−(1/4))+(−(1/4)−(π/8)) =−(1/2) .](Q20225.png)
Commented by Joel577 last updated on 24/Aug/17

Commented by Joel577 last updated on 24/Aug/17
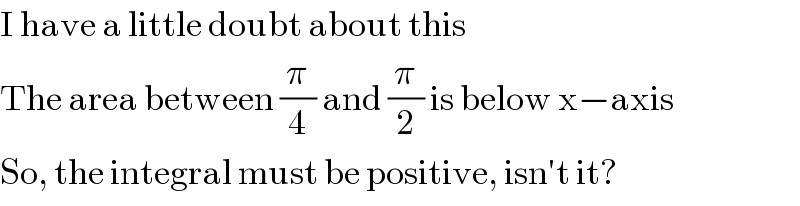
Commented by Joel577 last updated on 24/Aug/17
Commented by ajfour last updated on 24/Aug/17
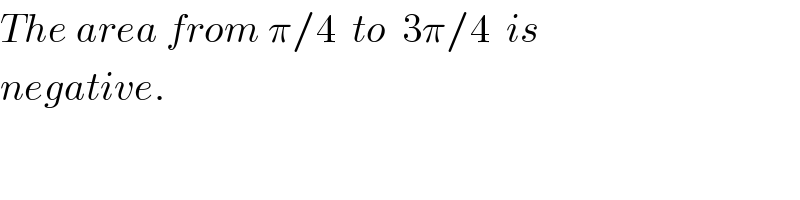
Commented by Joel577 last updated on 25/Aug/17