
Question and Answers Forum
Question Number 11862 by Mr Chheang Chantria last updated on 03/Apr/17

Answered by Joel576 last updated on 03/Apr/17
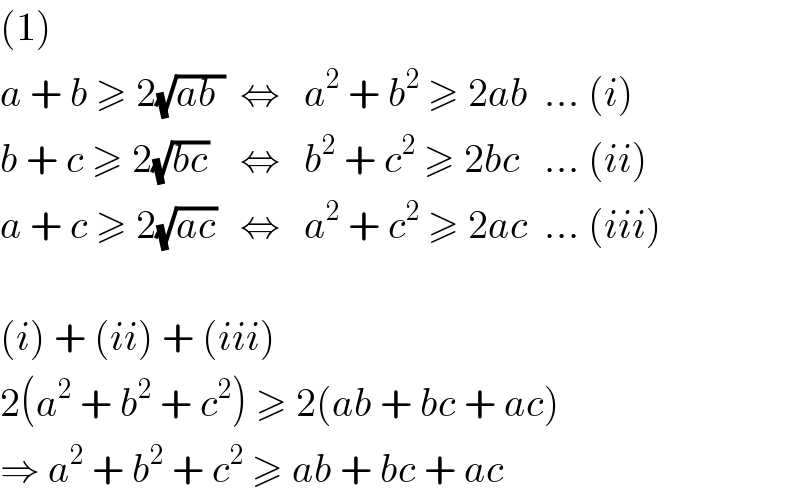
Answered by Joel576 last updated on 03/Apr/17
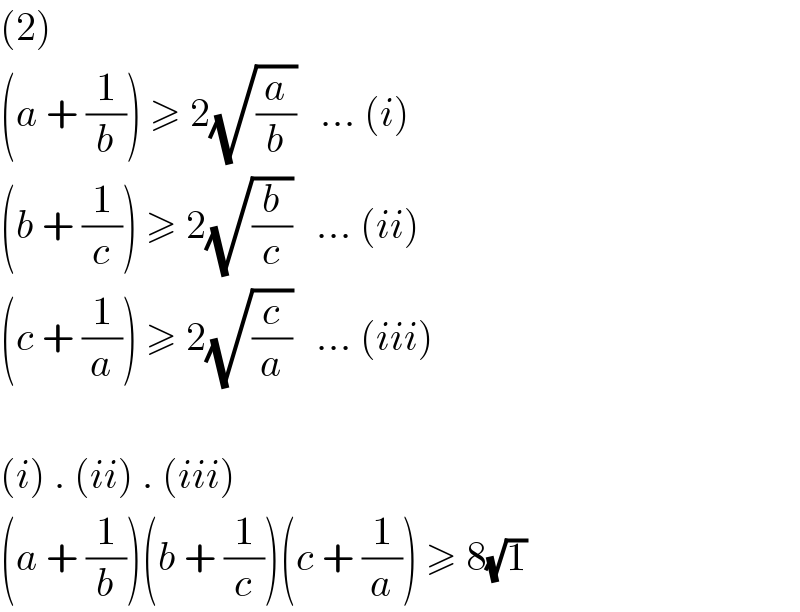
Commented by Mr Chheang Chantria last updated on 03/Apr/17

