
Question and Answers Forum
Question Number 74322 by naka3546 last updated on 22/Nov/19
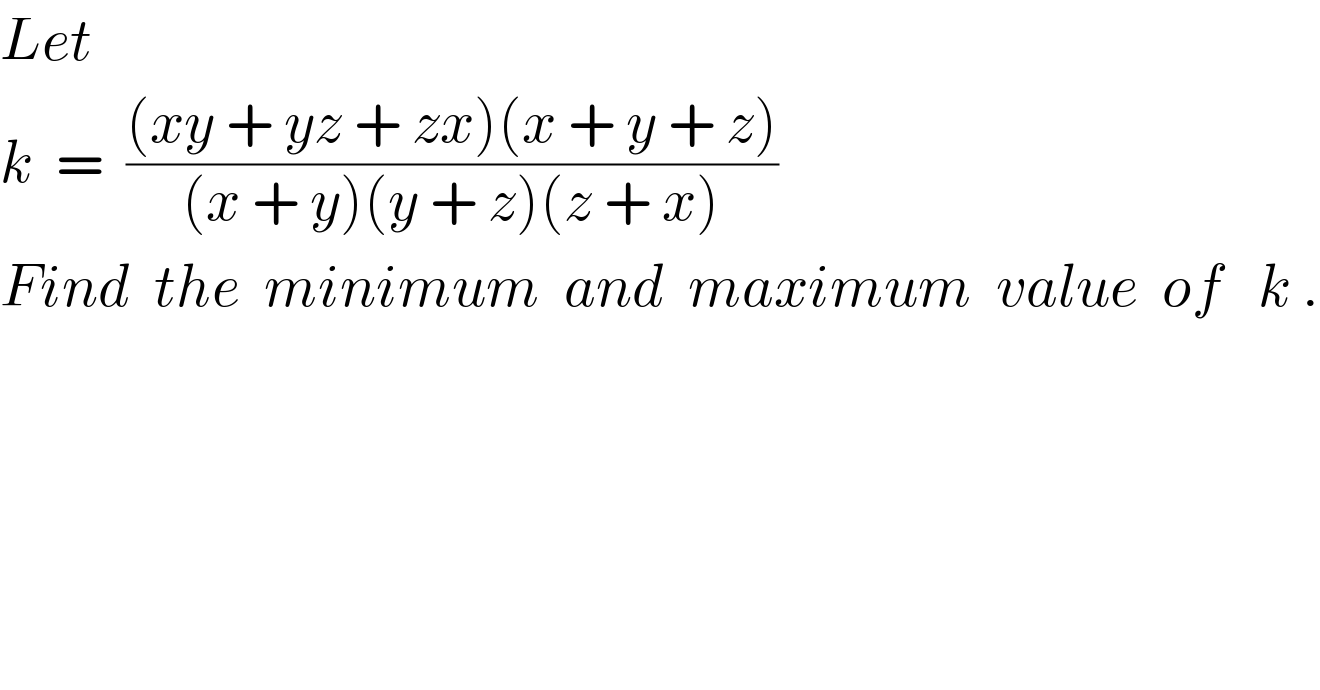
Answered by MJS last updated on 23/Nov/19
![k−1=((xyz)/((x+y)(x+z)(y+z))) y=px∧z=qx (1) k−1=((pq)/((p+1)(p+q)(q+1))) (d/dq)[((pq)/((p+1)(p+q)(q+1)))]=0 ((p(p−q^2 ))/((p+1)(p+q)^2 (q+1)^2 ))=0 ⇒ q=±(√p) insert in (1) k−1=(p/((1±(√p))^2 (p+1))) (d/dp)[(p/((1±(√p))^2 (p+1)))]=0 ((1±p^(3/2) )/((1∓(√p))^3 (p+1)^2 ))=0 ⇒ p=1∧q=1 (no other real solution) ⇒x=y=z ⇒ k−1=(1/8) ⇒ k=(9/8) which is the absolute maximum the minimum is −∞ put q=1: k−1=(p/(2(p+1)^2 )) lim_(p→−1) ((p/(2(p+1)^2 ))) =−∞](Q74375.png)
| ||
Question and Answers Forum | ||
Question Number 74322 by naka3546 last updated on 22/Nov/19 | ||
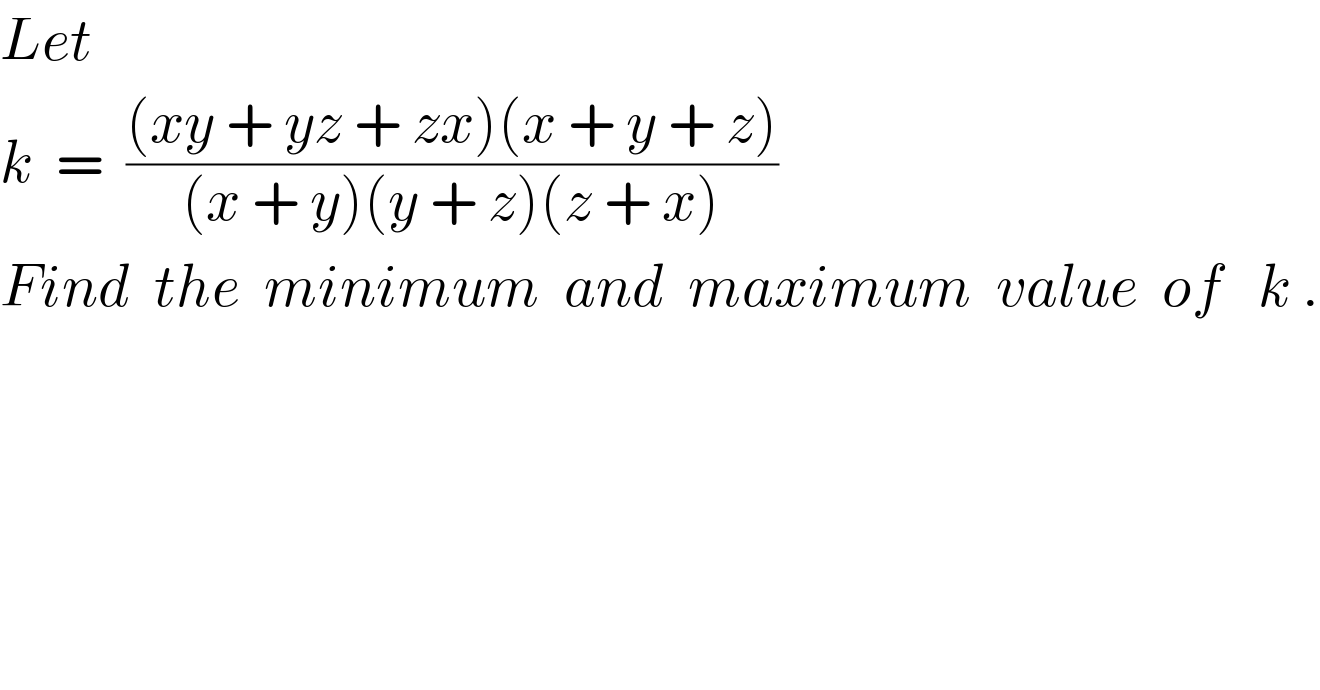 | ||
Answered by MJS last updated on 23/Nov/19 | ||
![k−1=((xyz)/((x+y)(x+z)(y+z))) y=px∧z=qx (1) k−1=((pq)/((p+1)(p+q)(q+1))) (d/dq)[((pq)/((p+1)(p+q)(q+1)))]=0 ((p(p−q^2 ))/((p+1)(p+q)^2 (q+1)^2 ))=0 ⇒ q=±(√p) insert in (1) k−1=(p/((1±(√p))^2 (p+1))) (d/dp)[(p/((1±(√p))^2 (p+1)))]=0 ((1±p^(3/2) )/((1∓(√p))^3 (p+1)^2 ))=0 ⇒ p=1∧q=1 (no other real solution) ⇒x=y=z ⇒ k−1=(1/8) ⇒ k=(9/8) which is the absolute maximum the minimum is −∞ put q=1: k−1=(p/(2(p+1)^2 )) lim_(p→−1) ((p/(2(p+1)^2 ))) =−∞](Q74375.png) | ||
| ||