
Question and Answers Forum
LogarithmsQuestion and Answers: Page 12
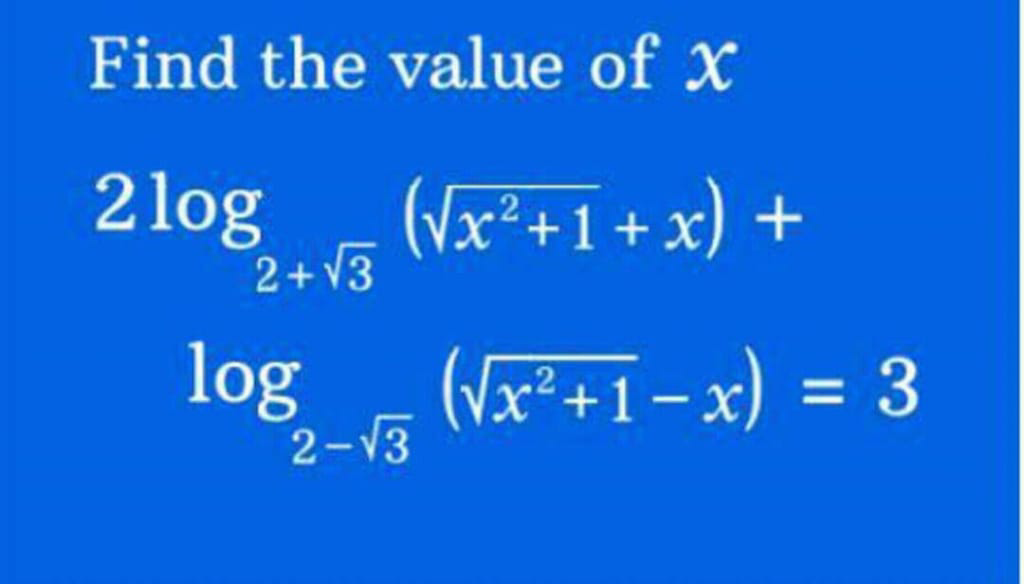
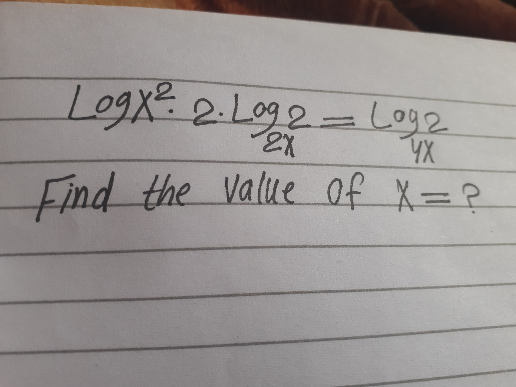
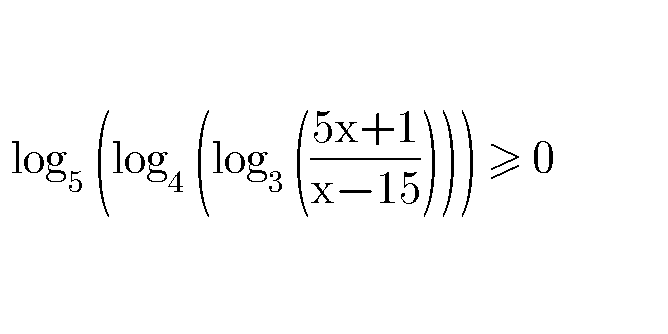


|
Question and Answers Forum |
LogarithmsQuestion and Answers: Page 12 |
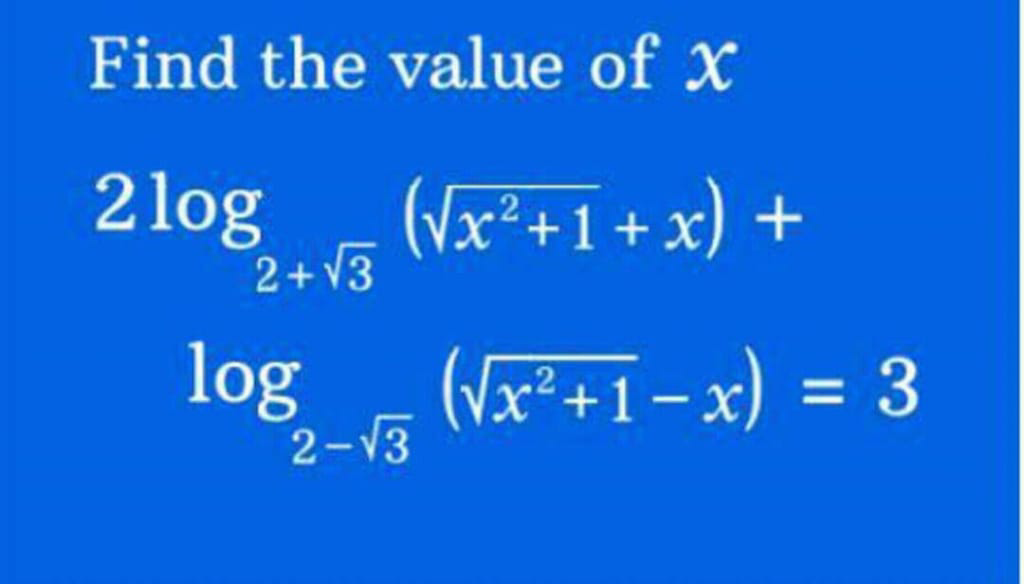
|
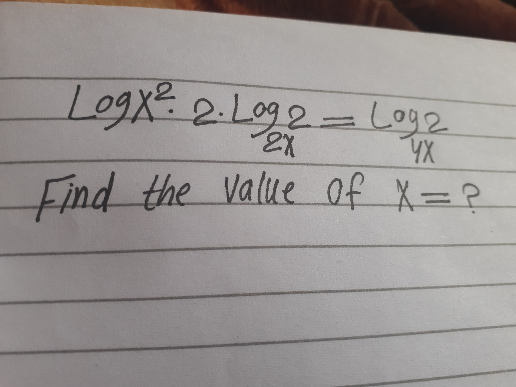
|
| ^3 log (^x^2 log (^x^2 log x^4 ))> 0 |
| ((∣x−3∣^(x+1) ))^(1/(4 )) = ((∣x−3∣^(x−2) ))^(1/(3 )) |
| find the solution of ((∣ log_2 (x)+2∣)/(x−3)) < 2 |
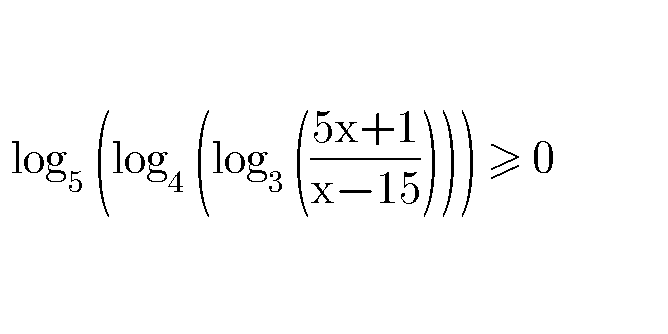
|
| log_2 (x) + log_3 (x) = 1 x = |
| 4^x +6^x =9^x |
| [4 |
| 3^(^(∣x∣) log 27) ≥ ((81)/x) |
| ^x log (xy).^y log (xy) +^x log (x−y).^y log (x−y)=0 find x+y |
| log_(((x/(x−3)))) (7) < log_(((x/3))) (7) |
| −log_(((x/6))) (((log_(10) (√(6−x)))/(log_(10) x))) > log_(10) (((∣x∣)/x)) |
| log_(0.5) ^2 (8+2x−x^2 )−7log_2 (8+2x−x^2 )<−12 |
| 5^((x+1)^2 ) + 625 ≤ 5^(x^2 +2) + 5^(2x+3) |
| log_3 (25x^2 −4)−log_3 (x) ≤ log_3 (26x^2 +((17)/x)−10) |
| (√(x^2 −2x+2)) + log_3 (√(x^2 −2x+10)) = 2 |
| ((6−log_(16) (x^4 ))/(3+2log_(16) (x^2 ))) < 2 |
| { ((log_(10) (x)+((log_(10) (x)+8log_(10) (y))/(log_(10) ^2 (x)+log_(10) ^2 (y)))=3)),((log_(10) (y)+((8log_(10) (x)−log_(10) (y))/(log_(10) ^2 (x)+log_(10) ^2 (y)))=0)) :} find x & y |
| ((log_((x−1)) (6x−1))/(((1/8)(log_3 (x^2 ))^3 −log_3 (x))(log_3 (x−2)−1))) ≥ 0 |

|
| (x^2 /(log_((5−x)) (x))) ≤ (5x−4) log_x (5−x) |
| Given 2(√(log_3 x−1)) − log_3 x^3 +8 > 0 have the solution a ≤ x < b. what is b ? |
| 4^x + 10^x = 25^x x = ? |

|
| log_(3+2x−x^2 ) (((sin x+(√3)cos x)/(sin 3x))) = (1/(log_2 (3+2x−x^2 ))) |