
Question and Answers Forum
LogicQuestion and Answers: Page 4



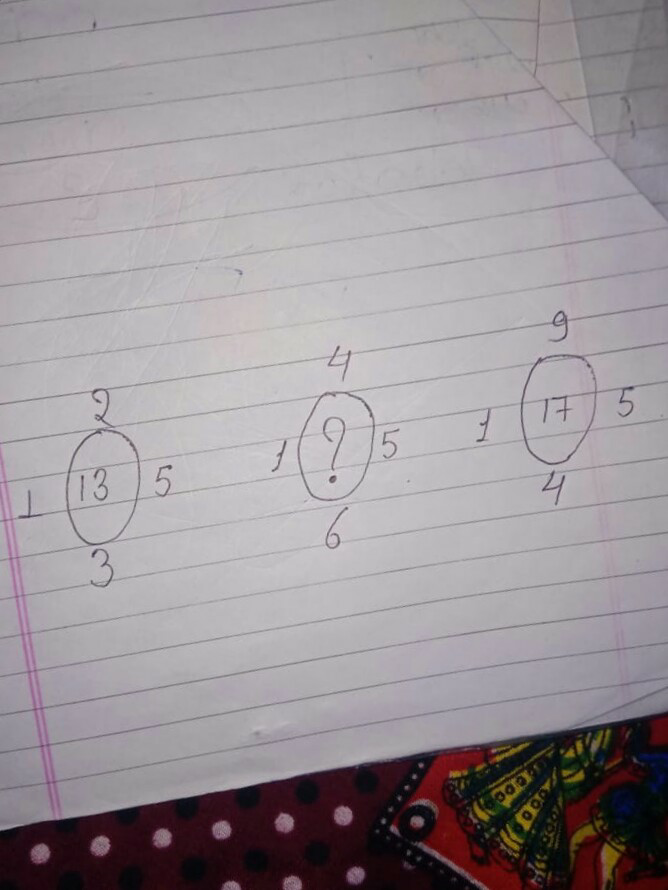

|
Question and Answers Forum |
LogicQuestion and Answers: Page 4 |

|
| In a Gregorian calendar, a year finishing with 00 is a leap year if only it′s vintage is divisible by 400. Also, the 1^(st) January 1900 was a Monday. 1\ Show that a year with the vintage finishing with 00 cannot begin on a Sunday 2\ Show that for a person born between 1900−2071, his 28 anniversary will occur on the same day of birth. |
| Show that if 3 prime numbers, all greater than 3, form an arithmetic progression then the common difference of the progression is divisible by 6. |
| what are the next two number of this series 4,7,9,2,5,6,3,8 ? |
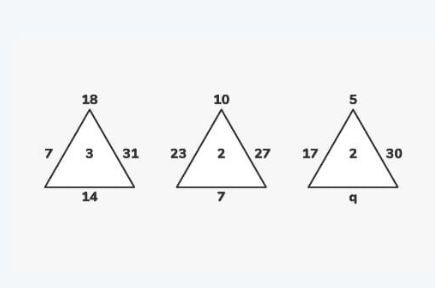
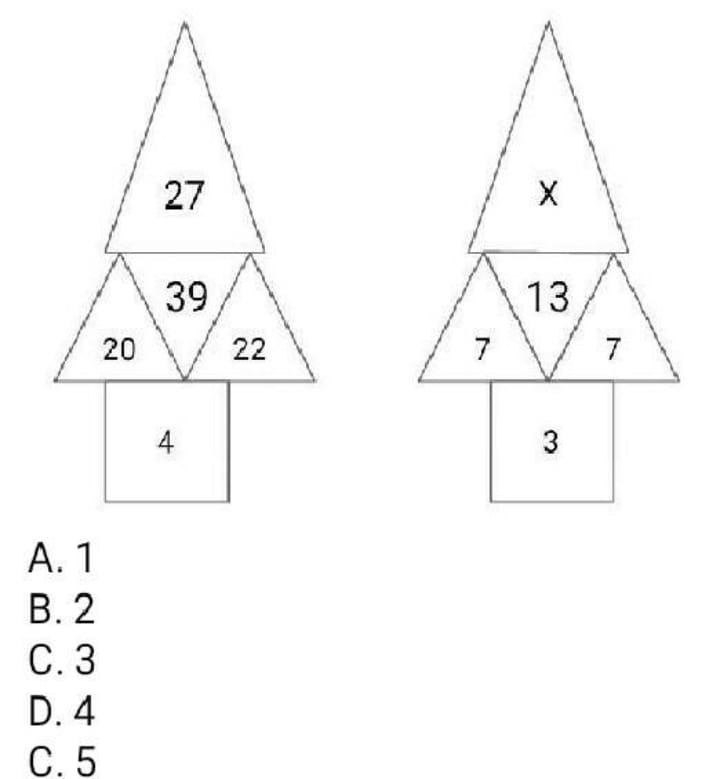
| 3,4,12,39,103,x (a) 164 (b) 170 (c) 172 (d) 228 |
| 26≡R_1 [37] 1 ≡R_2 [3] 2≡R_3 [5] Find R_1 , R_2 and R_3 |

|

|

|
| 2x^2 +5x+7=0 |
| prove p⇒q and ∼q⇒∼p are logicaly equivalent with out truth table |
| prove p⇒q and negetion of q⇒negation of p |

|

|
| Let A={2,4,6,7,8,9} B={1,3,5,6,10} and C={x:3x+6=0 or 2x+6=0}.Find a. A∪B. b. is(A∪B)∪C=A∪(B∪C)? |

|
| Prove that f(x) = x − a cos (x) − b has at least one real root for ∀a,b ∈ R |
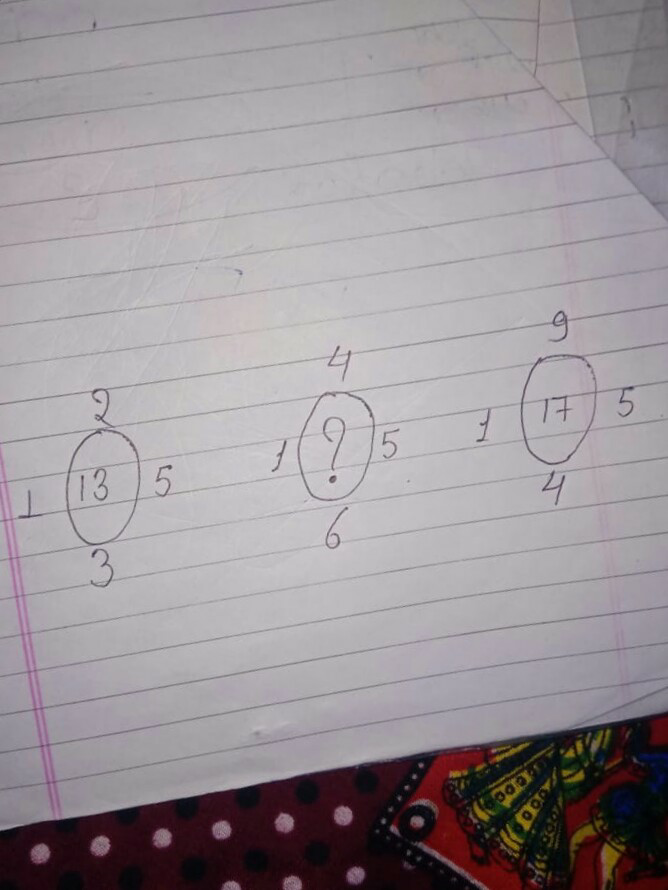
|
| Here are three propositions: − This sentence has exactly six words −There are two wrong propositions −The two previous sentences are correct Among that propositions ,how many are wrong? list them! |
| pour 1<k<n montrer que k(n+1−k)<(n+1/2)^2 |
| 1)Let consider S= Σ_(n=0) ^∞ n and T=Σ_(n=0) ^∞ (−1)^(n+1) n We know that ∀ x∈]−1;1] Σ_(n=0) ^∞ (−x)^n =(1/(1+x)) , then after derivating (1/((1+x)^2 ))=Σ_(n=1) ^∞ (−1)^(n+1) nx^(n−1) for x=1 ,we get T=(1/4) Now let ascertain something T=Σ_(n=0) ^∞ (−1)^(2n+2) (2n+1) +Σ_(n=0) ^∞ (−1)^(2n+1) (2n) =Σ_(n=0) ^∞ (2n+1) −2S (•) knowing that S=Σ_(n=0) ^∞ (2n)+Σ_(n=0) ^∞ (2n+1) So Σ_(n=0) ^∞ (2n+1)= S−2S When replacing that value in (•) we get T=(S−2S )−2S If i conclude that T=−3S and finally find S=−(T/3)=−(1/(12)) where will the mistake be? 2)Let consider K=1+((2020)/(2019))+(((2020)/(2019)))^2 +(((2020)/(2019)))^3 +......+... ((2020)/(2019))K=((2020)/(2019))+(((2020)/(2019)))^2 +(((2020)/(2019)))^3 +.... K−1=((2020)/(2019))+(((2020)/(2019)))^2 +(((2020)/(2019)))^3 +... So ((2020)/(2019))K=K−1 Then K=−2019 Where is the error? 3)Let consider n an integer We have 0=n−n =n+(−n)=n+(−n)^(2×(1/2)) =n+[(−n)^2 ]^(1/2) =n+ (√n^2 ) = n+n=2n So << all integer are null : 0 is the only integer>> Where is the error? 4) let consider n an integer different of zero and f(n)=nln(n) we have (df/dn)=ln(n)+1 (•) Likewise f(n)=ln(n^n ) and we know that n^n =n×n×n×......×n (n times) So f(n)=ln(n)+ln(n)+......+ln(n) (n times) Now we have (df/dn)=(1/n)+(1/n)+....+(1/n) (n times) So (df/( dn))=1 (••) Relation (•) and (••) give ln(n)+1=1 then ln(n)=0 ⇒ n=1 << The logarithm of all n≥1 is null : There is no integer big than 1 >> Where is the error? 5) let consider x=0,999999999....... we ascertain that 10x=9,999999999...... then 10x=9+0,999999999.... So 10x=9+x finally x=1 << 0.9999999999999999 ..... is and integer >> Is there any error? 6)let consider a=((26666666666666666)/(66666666666666665)) b=((999999999999999999999995)/(199999999999999999999999)) In the way to cancel , if i just remove one common figure to the numerator and to the denominator And i find a=(2/5) and b=(5/1) Will it be wrong? if no ,explain! |

|
| Answer: 0^0 =? |
| If a + b + c = 4 then find a^3 + b^3 + c^(3 ) = ? |
| Prove that Ln(z+1)=z−(z^2 /2)+(z^3 /3)−(z^4 /4)+... for ∣z∣< 1 |