
Question and Answers Forum
LogicQuestion and Answers: Page 5






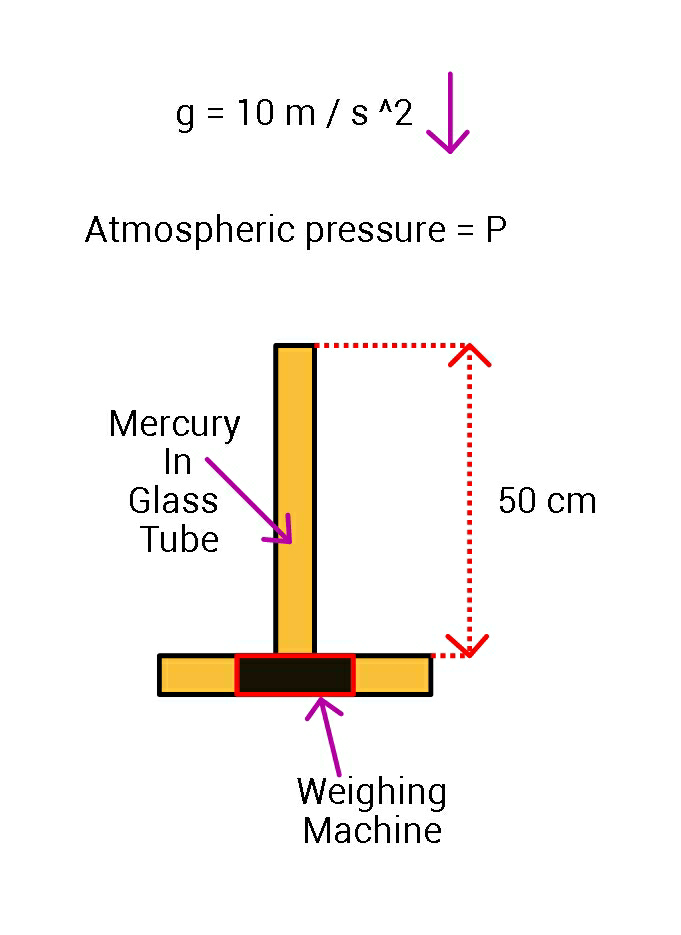



|
Question and Answers Forum |
LogicQuestion and Answers: Page 5 |

|

|
| Prove that if a, b, c ∈ Z and a^2 + b^2 = c^2 , then 3 ∣ ab |

|
| Is there a backwards “⇒”? |

|

|
| Solve: w^3 = − 16 |

|
| −2y(y−12)(y−1)or(y−12)(−2y^2 −2y) both are same. |

|

|

|
| Let Akbar and Birbal together have n marbles, where n > 0. Akbar says to Birbal, “If I give you some marbles then you will have twice as many marbles as I will have.” Birbal says to Akbar, “If I give you some marbles then you will have thrice as many marbles as I will have.” What is the minimum possible value of n for which the above statements are true? |
| A 4×4×4 wooden cube is painted so that one pair of opposite faces is blue, one pair green and one pair red. The cube is now sliced into 64 cubes of side 1 unit each. (i) How many of the smaller cubes have no painted face? (ii) How many of the smaller cubes have exactly one painted face? (iii) How many of the smaller cubes have exactly two painted face? (iv) How many of the smaller cubes have exactly three painted face? (v) How many of the smaller cubes have exactly one face painted blue and one face painted green? |
| A lotus plant in a pool of water is (1/2) cubit above water level. When propelled by air, the lotus sinks in the pool 2 cubits away from its position. Find the depth of water in the pool. |
| The accompanying diagram is a road- plan of a city. All the roads go east- west or north-south, with the exception of one shown. Due to repairs one road is impassable at the point X, Of all the possible routes from P to Q, there are several shortest routes. How many such shortest routes are there? |
| The base of a pyramid is an equilateral triangle of side length 6 cm. The other edges of the pyramid are each of length (√(15)) cm. Find the volume of the pyramid. |
| A distance of 200 km is to be covered by car in less than 10 hours. Yash does it in two parts. He first drives for 150 km at an average speed of 36 km/hr, without stopping. After taking rest for 30 minutes, he starts again and covers the remaining distance non-stop. His average for the entire journey (including the period of rest) exceeds that for the second part by 5 km/hr. Find the speed at which he covers the second part. |
| The Object shown in the diagram is made by gluing together the adjacent faces of six wooden cubes, each having edges of length 2 cm. Find the total surface area of the object in square centimetres. |
| In the diagram, it is possible to travel only along an edge in the direction indicated by the arrow. How many different routes from A to B are there in all? |
| Find distinct natural numbers from 1 to 9 such that these six equations are satisfied simultaneously: (1) a + bc = 20 (2) d + e + f = 20 (3) g − hi = −20 (4) adg = 20 (5) b + eh = 20 (6) c + f − i = 10 |
| order of a circle whose centre is origin and radius is r . |
| If z = x + jy , where x and y are real, show that the locus ∣((z − 2)/(z + 1))∣ = 2 is a circle and determine its centre and radius. |

|
| Let n be an odd positive integer. On some field, n gunmen are placed such that all pairwise distances between them are different. At a signal, every gunman takes out his gun and shoots the closest gunman. Prove that: (a) at least one gunman survives; (b) no gunman is shot more than 5 times; (c) the trajectories of the bullets do not intersect. |