
Question and Answers Forum
Matrices and DeterminantsQuestion and Answers: Page 11
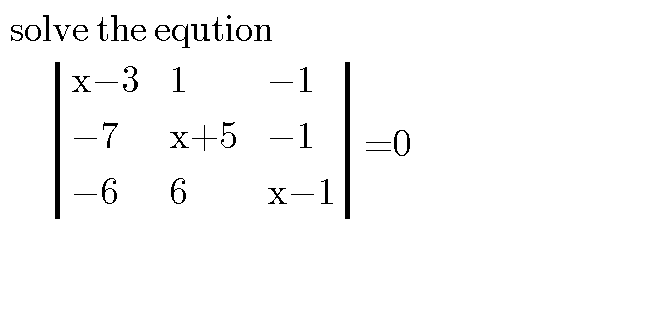







|
Question and Answers Forum |
Matrices and DeterminantsQuestion and Answers: Page 11 |
| reduce the matrix below to echelon form and then to row canonical form A = [((2 4 2 −2 5 1)),((3 6 2 2 0 4)),((4 8 2 6 −5 7)) ] |
| A= [(1,(−1)),((−4),(−2)) ] A^(2016) =.....? |
| u= [(1,(−1),2) ] A= [(3,2),(1,3),(0,1) ] v= [(2,(−1)) ] uAv^t =....? |
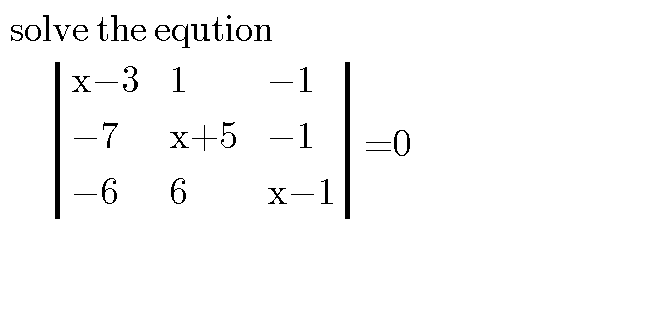
|
| prove that determinant ((1,1,1),(x,y,z),(x^2 ,y^2 ,z^2 ))=(x−y)(y−z)(z−y) |
| solve the eqution determinant (((x−3),1,(−1)),((−7),(x+5),(−1)),((−6),6,(x−1)))=0 |

|
| find the determinant of the matrix below determinant ((0,4,0,0,0),(0,0,0,2,0),(0,0,3,0,0),(0,0,0,0,1),(5,0,0,0,0)) |
| find the determinant of the matrix below determinant ((0,0,0,0,1),(0,0,0,2,0),(0,0,3,0,0),(0,4,0,0,0),(5,0,0,0,0)) |
| find the determinant of the matrix below [(1,4,(−3),1),(2,0,6,3),(4,(−1),2,5),(1,0,(−2),4) ] |
| Find the determinant of the matrix below. determinant (((3 1 5 3)),((4 3 8 5)),((6 2 1 7)),((8 5 8 1))) |

|

|

|

|

|
| Prove that the set of all m × n matrices having entries in a field is a vector space over F. |
| 3x−2y−4z=2 3y−4z=−2 2y+6z=−1 |
| for what value of k the system of equation has no solution x+2y+3z=1 2x+ky+5z=1 3x+4y+7z=1 |
| i |

|
| Let P= (((1−p_1 ),p_2 ),(p_1 ,(1−p_2 )) )= ((a_(1,1) ,a_(1,2) ),(a_(2,1) ,a_(2,2) ) ) and that P^n be the nth power of P evaluated as P^n =P×P^(n−1) ;i.e by successive pre−multiplication of P to P^2 ,P^3 ,P^4 ,... up to P^(n−1) . Show that the element of P^n in the second row and first column is a_(2,1) =((p_1 (1−(1−p_1 −p_2 )^n ))/(p_1 +p_2 )). {The columns of P^n represent probability vectors for all n∈N. Hence, a_(1,1) +a_(2,1) =1 and a_(1,2) +a_(2,2) =1 for example.} |
| ∫_(−∞) ^∞ ∫_(−∞) ^∞ (√(x^2 +y^2 ))exp(((−1)/2)(x^2 +y^2 ))dydx=? |
| Find det(A) where A is an n×n matrix of the form A= ((λ,1,1,…,…,…,…,1),(1,λ,1,…,…,…,…,1),(1,1,λ,…,…,…,…,1),(⋮,⋮,⋮,⋱,…,…,…,1),(⋮,⋮,⋮,⋮,⋱,…,…,1),(⋮,⋮,⋮,⋮,⋮,⋱,…,1),(⋮,⋮,⋮,⋮,⋮,⋮,⋱,1),(1,1,1,1,1,1,1,λ) ) λ=constant for leading diagonal elements 1s for all other elements. |
| Let A= ((a,b),(c,d) ). Find a condition on a,b,c,d so that A^(n+1) −A^n =nA, n∈N. A^(n+1) −A^n =nA A^n −A^(n−1) =(n−1)A A^(n−1) −A^(n−2) =(n−2)A A^(n−2) −A^(n−3) =(n−3)A ... A^4 −A^3 =3A A^3 −A^2 =2A A^2 −A=A So, A^(n+1) −A=(n+n−1+n−2+...+3+2+1)A A^(n+1) =A+((n(n+1))/2)A A^(n+1) =((n^2 +n+2)/2)A A^n =(((n−1)^2 +n+1)/2)A A^n =((n^2 −n+2)/2)A (n≥1), A= ((a,b),(c,d) ) . |
| A= [(1,2),(2,5) ],B= [(3,(−1)),(4,(+2)) ] determine A^B |