
Question and Answers Forum
Matrices and DeterminantsQuestion and Answers: Page 5





|
Question and Answers Forum |
Matrices and DeterminantsQuestion and Answers: Page 5 |
| Given A a 3x3 matrix satisfy → { ((A ((1),(2),(3) ) = ((3),(4),(2) ))),((A ((5),(9),(7) ) = ((3),(1),(2) ))) :} . Find A (((10)),((18)),((14)) ) ? |
|
| if matrix A^2 = (((1 3)),((0 1)) ) then matrix A=... |

|
| Given a matrix A= (((−1 3 2)),(( 0 1 4)),((−2 3 2)) ) and A^(−1) = (1/(10))(kA+9I−A^2 ). find k. |
| find determinant (((((a^2 +b^2 )/c) c c)),(( a ((b^2 +c^2 )/a) a)),(( b b ((a^2 +c^2 )/b))))=? |
| consider a non−singular 2×2 square matrix T. If trace (T) =4 and trace (T^2 )=5 what is determinant of the matrix T ? |

|
| Find an orthogonal matrix A whose first row is u_1 = ((1/3), (2/3), (2/3)). |
| Solving by Gaussian elimination using the following system of linear equation { ((x−3y−2z=6)),((2x−4y−3z=8)),((−3x+6y+8z=−5)) :} |

|
| solve for x determinant (((1 x x^2 x^3 )),((1 2 2^2 2^3 )),((1 3 3^2 3^3 )),((1 4 4^2 4^3 )))= 0 |
| Given matrix A = (((a 1 1)),((1 a 1)),((1 1 a)) ) If B = b.A and B is orthogonal determine value of a and b. |
| If determinant (((a a^2 1+a^3 )),((b b^2 1+b^3 )),((c c^2 1+c^3 )))= 0 a≠b≠c → { ((a =?)),((b=? )),((c=?)) :} |
| If the product of the matrices (((1 1)),((0 1)) ) (((1 2)),((0 1)) ) (((1 3)),((0 1)) )... (((1 k)),((0 1)) )= (((1 378)),((0 1)) ) then k = |

|
| Given a matrix A = (((a b)),((c d)) ) satisfies the equation A^2 +λA+7I = 0 where I= (((1 0)),((0 1)) ) . Find the value of trace of A |
| Given matrix A= (((1 0)),((2 3)) ) , B= (((−1 −3)),(( 2 0)) ) and AX +2B = I . what the value of det (X) ? |
| ((♭emath)/(•••••)) use cayley − hamilton theorem to calculate A^(−1) for A= (((1 2 2)),((1 2 −1)),((−1 1 4)) ) |
| ((♥JS♥)/(°js°)) Given a matrix A= ((( 3 2)),((−5 −4)) ) and A^2 +♭A−2I=0 where ♭ is a constant , I= (((1 0)),((0 1)) ). If B = (((−3♭ 2)),(( 5♭ −1)) ) , then A^(−1) B = |
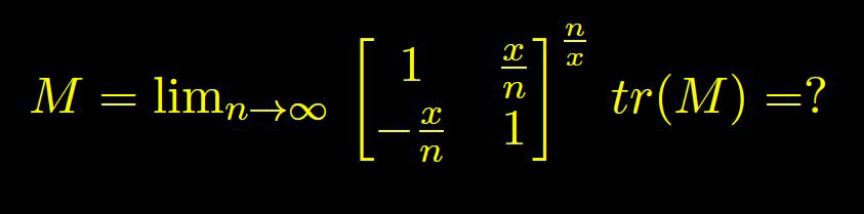
|
| How many different words can be formed with the same letters as in TINKUTARA if no two same letters are next to each other. |

|
|
| Given a = Σ_(n=1) ^(24) (1/((√(n+1))+(√n))) then the value of a + (1/(log _a (bc)+1)) + (1/(log _b (ac)+1)) + (1/(log _c (ab)+1)) = ? |
| [(1,5,3),(4,6,7),(9,2,8) ]+ [(9,5,7),(6,4,3),(1,8,2) ] |