
Question and Answers Forum
Matrices and DeterminantsQuestion and Answers: Page 7








|
Question and Answers Forum |
Matrices and DeterminantsQuestion and Answers: Page 7 |
| Make 2 3×3 matrices i and j such that i^2 =j j^2 =i ij=−1 |

|
| given A a square matrix non singular A≠ I. find A such that A^3 = I |
| let A= [((a b)),((c d)) ]use the augmented matrix[A I] and elementary row operation to show A^(−1) = (1/(ad bc)) [((a b)),((c d)) ]and show that det(A^(−1) )=(1/(det(A))) |
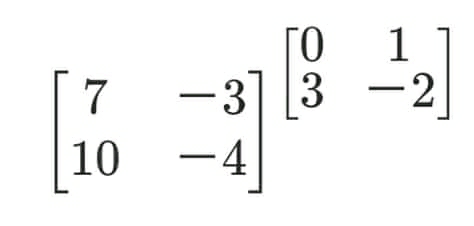
|
| Given that A and B are 3 × 3 invertible matrices, then (A^(−1) B)^(−1) = A. AB^(−1) B.B^(−1) A C. B^(−1) A^(−1) D. BA^(−1) |
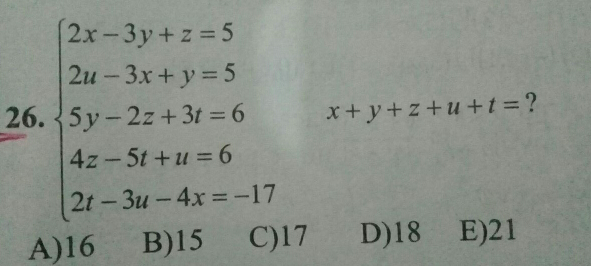
|
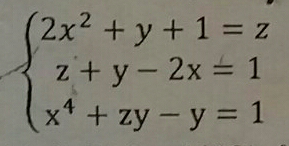
|
| Given the matrix A = ((1,(−1),1),(0,2,( −1)),(2,3,0) ) and B= ((3,3,(−1)),((−2),(−2),1),((−4),(−5),2) ) find the matrix product AB and BA state the relationship between A and B find also the matrix product BM, where M= ((8),((−7)),(1) ) Hence solve the system of equations: x−y + z = 8, 2y −z =−7, 2x + 3y = 1. |
| please state Cramer′s rule |

|
| A= (((1 2)),((0 1)) ) find A^n |
| Let d_n be the determinant of the n×n matrix whose entries, from left to right and then from top to bottom, are cos 1, cos 2, ..., cos n^2 . (For example, d_3 = determinant (((cos 1 cos 2 cos 3)),((cos 4 cos 5 cos 6)),((cos 7 cos 8 cos 9))). The argument of cos is always in radians not degrees.) Evalue lim_(n→∞) d_(n.) |

|
| (√(2014))x^3 −4029x^2 +2=0 x_1 <x_2 <x_3 x_2 (x_1 +x_3 )=? |

|
| f0f=θ |
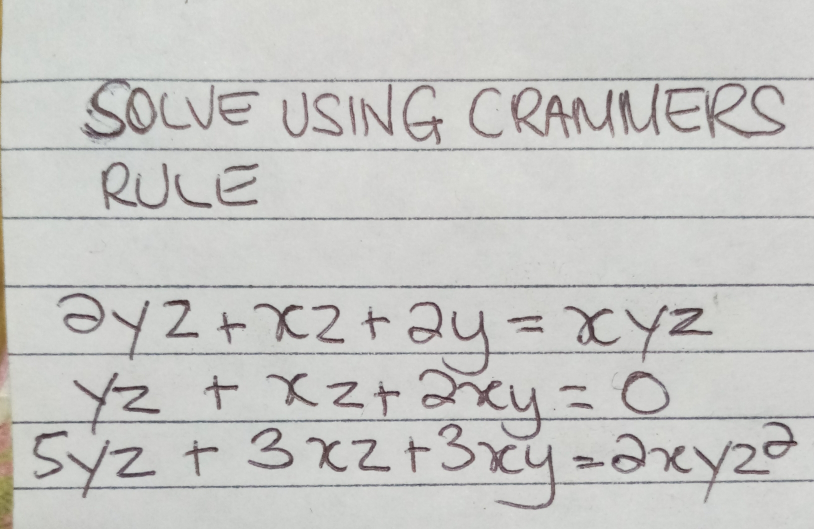
|

|
| Let A be3×3 matrix with eigen values 1,−1,0. Then determinant of I+A^(100 ) =?? |

|

|

|
| find all second order partial derivatives f(x,y)=xe^x^y .y^x |
| Find the image of y=3x+1 under the mapping (((2 3)),((1 2)) ). |