
Question and Answers Forum
Matrices and DeterminantsQuestion and Answers: Page 9








|
Question and Answers Forum |
Matrices and DeterminantsQuestion and Answers: Page 9 |
| Let A= (((1 3)),((2 5)) ). Find an expression for the enteries of A^n . |
| A and B are two non−singular matrices such that A^6 =I and AB^2 =BA(B≠I). Then value of K for which B^K =I. |
| Let A,B be two n×n matrices such that A+B=AB then prove : AB=BA ? |
| reduce this matrix [(2,3,4,1),(1,7,2,3),((−1),4,2,0),(0,1,1,0) ] |
| Find LCM [((13)/2),(2/(13)),(4/7)] [((57)),(0) ]× |
| Let A be 2×3 matrix , whereas B be 3×2 matrix. If determinant(AB)=4, then the value of determinant (BA) ? |

|
| If both A− (I/2) and A+(I/2) are orthogonal matrices, then prove that A^2 = −(3/4) I. |
| In Matrices, Is (A^(−1) )B = B(A^(−1) ) ? |
| If A is a square matrix of order 3, then ∣(A−A^T )^(2011) ∣ = ? |

|

|
|

|

|
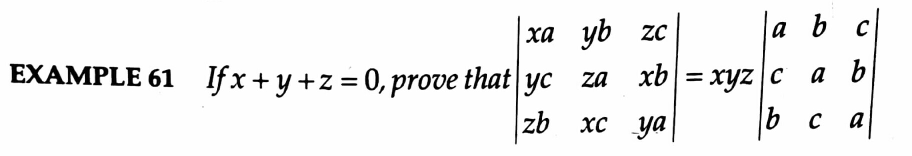
|

|

|

|
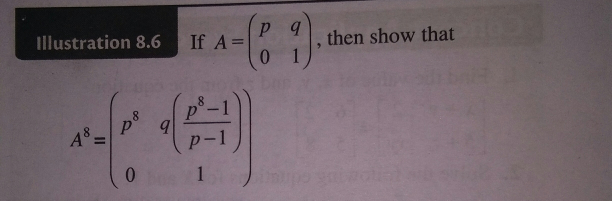
|
| A= [(α,1,1,1),(1,α,1,1),(1,1,β,1),(1,1,1,β) ]with α^2 ≠1≠β^2 det(A)=....??? |
| [(2,1),(0,2) ]^(2018) =.....??? |
| A= [((1 5)),((6 7)) ]find A^k |
| Prove that determinant ((3,(a+b+c),(a^2 +b^2 +c^2 )),((a+b+c),(a^2 +b^2 +c^2 ),(a^3 +b^3 +c^3 )),((a^2 +b^2 +c^2 ),(a^3 +b^3 +c^3 ),(a^4 +b^4 +c^4 ))) =(a−b)^2 (b−c)^2 (c−a)^2 |
| let give A = ((( 1 1 0)),((0 1 1)) ) (1 0 1 ) calculate A^n and e^(−A) . |
| let give A = (((0 1 0)),((0 0 1)) ) (1 0 0 1) find A^3 2) find e^(tA) . |