
Question and Answers Forum
Number TheoryQuestion and Answers: Page 7

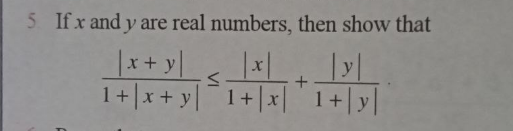




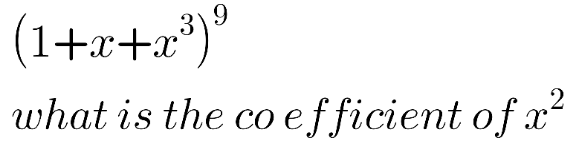

|
Question and Answers Forum |
Number TheoryQuestion and Answers: Page 7 |
| Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^3 ))=? |
| how many positive x≤10 000 integers are such that 2^x −x^2 is divisible by 7? |
| The value of Σ_(n=0) ^∞ (((3_n )(2_n )x^n )/((1_n )n!)) β(2,n+1) is a. (1/2)Σ_(n=0) ^∞ (2_n )(x^n /(n!)) b. (1/2)Σ_(n=0) ^∞ (((3_n )(2_n ))/((1_n ))) (x^n /(n!)) c. (1/2)Σ_(n=0) ^∞ (((2_n )x^n )/((1_n )n!)) d. (1/3)Σ_(n=0) ^∞ (((3_n )x^n )/((1_n )n!)) |
| Given a set consisting of 22 integer A={±a_1 ,±a_2 ,...,±a_(11) }. Show that exist subset of S with properties (1) for every i=1,2,3,...,11 have least one between a_i or −a_i element of S (2)the sum all possible numbers in S divisible by 2015 |

|
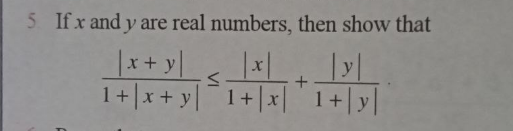
|

|

|

|
| ⌊x⌋+⌊y⌋=43.8 and x+y−⌊x⌋=18.4 .Find 100(x+y). |
| Let complex number z=(a+cos θ)+(2a−sin θ)i . If ∣z∣ ≤2 for any θ∈R then the range of real number a is ___ |

|
| ∫_0 ^x ⌊u⌋(⌊u⌋+1)f(u)du=Σ_(n=1) ^(⌊x⌋) n∫_n ^x f(u)du Prove that |
| How many digits will there be in 875^(16) ? |
| Π_(n=1) ^∞ (1+(x^3 /n^3 )) |
| φ(n^4 +1)=8n φ:Euler totient function Solve for n∈N |
| Prove that 𝛗(n)=nΠ_k (1−(1/p_k )) φ(n):Euler totient function |
| (((0 sin(x))),((0 0)) )!+ (((0 sin(2x))),((0 0)) )!+ (((0 sin(3x))),((0 0)) )!+... n^(th) term |
| log((((√5)+1)/(10))9e^γ )=((ζ(2))/2)(((1^2 +9^2 )/(10^2 )))−((ζ(3))/3) (((1^3 +9^3 )/(10^3 )) )+((ζ(4))/4)(((1^4 +9^4 )/(10^4 )))−... γ=Euler Mascheroni Constant |
| Determine if the series Σ_(n=1) ^∞ a_n defined by the formula converges or diverges . a_1 = 4 , a_(n+1) = ((10+sin n)/n). a_n |
| If 4x=3(Mod 6), find the first four values of x. |
| x^(⌊x⌋) + x^(⌈x⌉) = ((175)/8) |
| Find the first four values of 2x+5=1(mod 7) |
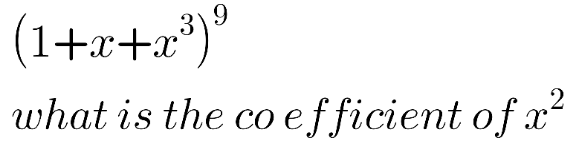
|
| Σ_(n_1 +2n_2 +3n_3 +..+rn_r =n) ^n (1/(n_1 !n_2 !n_3 !..n_r !1^n_1 2^n_2 3^n_3 4^n_4 ...r^n_r ))=1 0≥n_1 ,n_2 ,n_3 ,..≥n Prove the above identity |

|