
Question and Answers Forum
OthersQuestion and Answers: Page 120
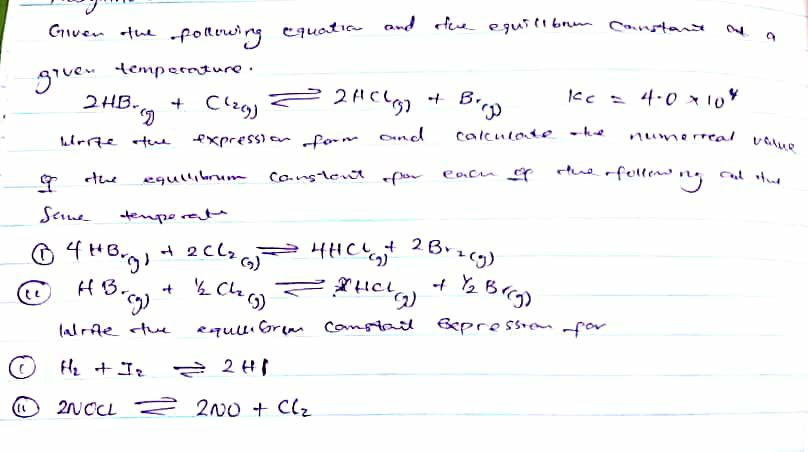



Pg 115 Pg 116 Pg 117 Pg 118 Pg 119 Pg 120 Pg 121 Pg 122 Pg 123 Pg 124
|
Question and Answers Forum |
OthersQuestion and Answers: Page 120 |
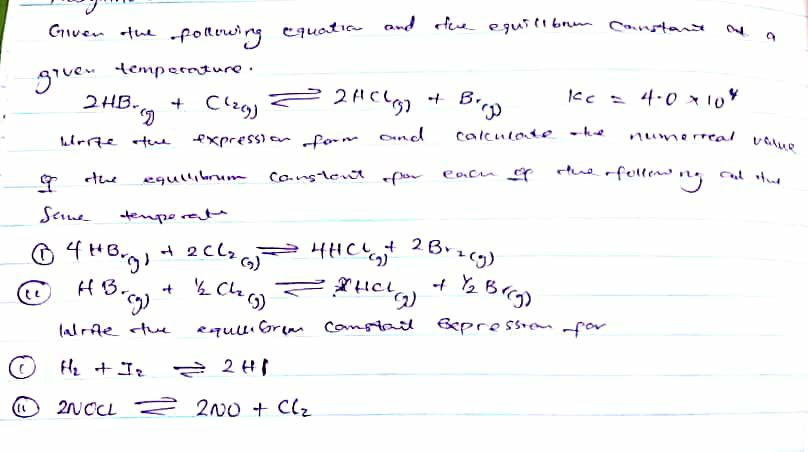
|
| ∫(((x−1)dx)/((x+1)(√(x^3 +x^2 +x)))) |
| (4) Find the term indepen− dent of x in the expansion of (x^2 −2+(1/x^2 ))^6 |
| (3) Find the term independ− ent of x in the expansion of ( x+(1/x))^2 (x−(1/x))^(12) |
| (2) Find the term indepen− dent of x in the expansion of (2x^2 +(1/x))^6 |
| (1) Find the term independent of x in the expansion of (x−(2/x))^(10) |
| A glass bottle full of mercury has mass 500g. On being heated through 35°C, 2.43g of mercury are expelled. calculate the mass of mercury remaining in the bottle (Cubic expansivity of mercury is 1.8 × 10^(−4) per K. linear expansivity of glass is 8.0 × 10^(−6) per K. |
| Write the series,indicating the 5th term,the 5th partial sum 0+1+3+...+(((n^2 +n)/2))+... |
| Write the first five series indicating the 5th term,5th partial sum Σ_(n=1) ^∞ t_n , where t_n = { ((1 for n=1)),(((1/2) for n=2)),((1−(1/2)+...+(−1)^(n+1) ((1/n)) for n>2)) :} |
| Δ=(√(m×φ)) Δ=mass gap m=mass φ=phi calculate phi to the same number of decimal places as the mass. use the mass of an electron |
| let give the equation x^6 −x−1=0 by using Newton methodfind the approximate value of the real?root for this equation. |
| Find the value of i^i ? |
| m_1 s_1 (x−𝛉)=m_2 s_2 (𝛉−y) ; x=? ;y=? 𝛉=? solve it as an equation.... |

|
| A 2000kg space capsule is traveling away from the earth, determine the gravitational field strenght and gravitational force on the capsule due to the earth when it is (a) At a distance from the earth′s surface equal to the radius of the earth (b) At a very large distance away from the earth (Take g = 9.8Nkg^(−1) on earth surface) |
| A particle of mass 2kg moves in a force field depending on a time t given by F = 24t^2 i + (36t − 16)j − 12tk assuming that at t = 0 the particle is located at r_0 = 3i − j + 4k and has v_0 = 6i + 5j − 8k. Find (a) Velocity at any time t (b) Position at any time t (c) τ (torgue) at any time t (d) Angular momentum at any time t above the Origin |
| Find the workdone in moving an object along a vector r = 3i + 2j − 5k if the applied force is F = 2i − j − k |
| A and B are walking along a circular track.They start from same point at 8:00 am. A can walk 2 rounds per hour and B can walk 3 rounds per hour. How many times they cross each other before 9:30 am if they walk (i) Opposite to each other. (ii) In same direction. ? |
| if 2 chords of ellipse have the same distance from the centre of ellipse and the eccentric angle of the end points of the chords are respectivly α β γ δ then prove that tan (α/2)×tan (β/2)×tan (γ/2)×tan (δ/2)=1 |
| (q_1 /q_2 )=((x/(0.8−x)))^2 ; x=? |

|
| L^(−1) ((s^3 /(s^4 +4)))=? |

|

|
| if g(x)=f(x)+f(1−x) and f^((2)) (x)<0 then show that g(x) is increasing in (0,1/2) and g(x) is decreasing in (1/2,1) |
| (√(1−x^(6 ) )) +(√(1−y^6 )) =k^3 (x^3 −y^3 ) then prove that (dy/dx)=((x^2 (√(1−x^2 )))/(y^2 (√(1−y^(2Δ) )))) |
Pg 115 Pg 116 Pg 117 Pg 118 Pg 119 Pg 120 Pg 121 Pg 122 Pg 123 Pg 124 |