
Question and Answers Forum
OthersQuestion and Answers: Page 29

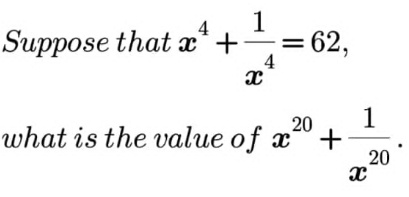






|
Question and Answers Forum |
OthersQuestion and Answers: Page 29 |
| If the Real component of an analytic function is given by log_e (x^2 +y^2 )^(1/2) , find the function. Mastermind |
| Given that U=x^4 −6x^2 y^2 +y^4 , find v and w such that w=u+iv is analytic Mastermind |

|
| Differentiate w.r.t ′x′ x^y +y^x =c Mastermind |
| The equation of the curve is given y=(x^3 /6)−((5x^2 )/2)−6x−1 1) Determine the critical points 2) Distinguish between these points 3) Determine the Maximum and minimum values 4) Determine the value of x and y at point of inflexion Mastermind |
| (√x)+1=0 find x Mastermind |
| Differentiate from first principle y=log_x a Mastermind |
| Show that the differential equation y′′ −4y′+4y=0 is satisfied when y=xe^(2x) Mastermind |
| ∫tan(2x+3)dx Mastermind |
| Differentiate from first principle y=(1/(x^2 +5)) |
| Differentiate wrt x y=sin^(−1) (2x+1) Mastermind |
| Show that substituting y=vx, x+y(dy/dx)=x(dy/dx)−y to a separable equation for v and x and its solution is log_e (x^2 +y^2 )=2tan^(−1) ((y/x)) +C Mastermind |
| Obtain the differential equation associated with the primitive y = Ae^(2x) +Be^x +C Mastermind |
| Show that if y=C_1 sinx + C_2 x then (1+xcotx)(d^2 y/dx^2 )−x(dy/dx)+y=0 Mastermind |
| lim_(x→∞) (((1+(√(x+2)))/(1−(√(x+2))))) Mastermind |
| Differentiate the following wrt x 1) y=x^x 2) y=sin^(−1) (2x+1) Mastermind |
| Given that: x cos y=sin(x+y), find (dy/dx) Mastermind |
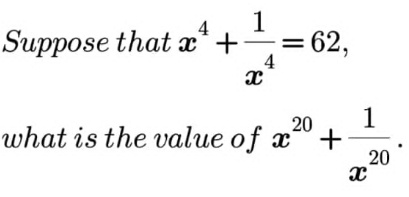
|

|

|

|

|
| Resolve 1) (x−y)ydx−x^2 dy=0 2)(2x−y)dx+(4x−2y+3)dy=0 |
| Resolve (1−x^2 y)dx+(x^2 y−x^3 )dy=0 ; μ=μ(x) |

|

|