
Question and Answers Forum
OthersQuestion and Answers: Page 34
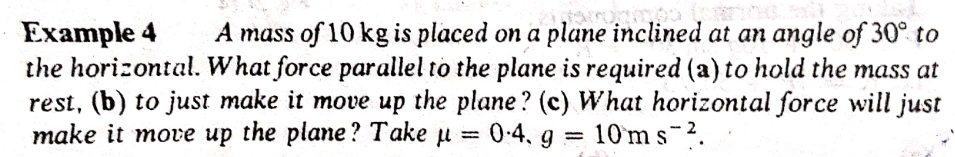






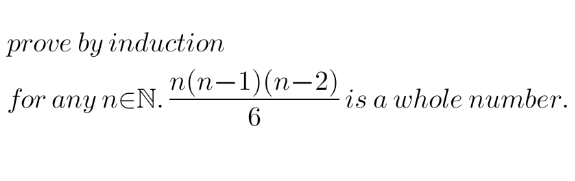

|
Question and Answers Forum |
OthersQuestion and Answers: Page 34 |
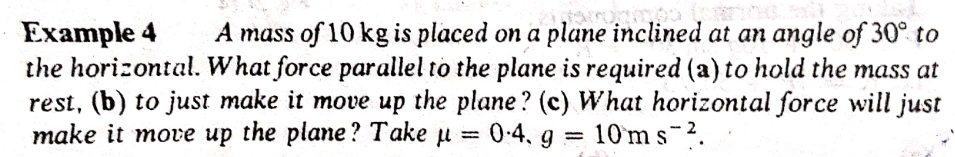
|
| Resolve 1. u_(n+2) −2u_(n+1) +4u_n =3^n with u_o =1, u_1 =−2 2. u_n =u_(n−1) −u_(n−2) +2sin (((nΠ)/3)) with u_o =1, u_1 =2 |

|

|
| U_(n+1) =(1/2)(u_n +(a/u_n )) with u_1 >0, a>0 Prove that (u_(n+1) /u_n )≤1 |
| Resolve I_n =∫_(−1) ^1 (1−x^2 )^n dx |
| Prove by absurd that log 2 is the number irrational |

|
| 1) Prove by recurrence that for n≥28, n!≥11^n 2) On subtract the limit of the suite (((n!)/(10^n ))) when n tended at +∞ |

|
| 1. Prove by recurrence that so n ∈ N and θ ∈ R (cos (nθ)+isin (nθ)=cos (nθ)+isin (nθ) 2. Prove that U_(n+1) =(1/5)(U_n ^2 +6) and U_1 =(5/2), is decrease |
| 1) Prove by absurd that ((ln 2)/(ln 3)) is irrational 2) Prove by absurd that (√2)+(√(6 ))≤(√(15)) |
| I_n =∫_(−1) ^1 (1−x^2 )^n cos ((a/(2b))x)dx to integrating by piece for n≥2 proven (a^2 /(4b^2 ))I_(n ) =2n(2n−1)I_(n−1) −4(n−1)I_(n−2) proven by rearring that ((a/(2b)))^(2n+1) I_n =n![p((q/(2b)))sin ((a/(2b)))+Q((a/(2b)))cos ((a/(2b)))] |
| Resolve the system d′ unknow (x, y,z) ∈ ⊂^3 x+y+z=1 x^2 +y^2 +z^2 =1 x^3 +y^3 +z^3 =−5 |
| what is 1(1/2)% |
| resolve ∫ln (cos x)dx |

|
| I_(n ) =∫_0 ^1 (x^(2n+1) /( (√(1+x^2 ))))dx , n≥0 prove that ∀ n≥0 (2n+1)I_n =(√2)−2nI_(n−1) |

|
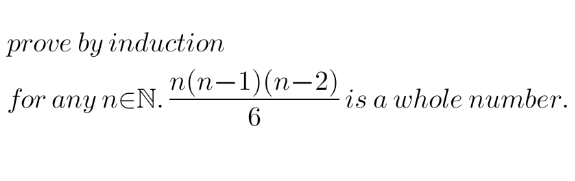
|
| 1) Proven that by all n ∈ N^∗ 2!4!..(2n)!≥((n+1)!)^n 2) Proven by recurring that Σ_(p=1) ^n pp!=(n+1)!−1 |
| find fourier′s serie of f(x)=x−[x] |
| what is the latest version of this app available i m having 2.265 |
| { ((a_1 =((√3)/2))),((a_(n+1) =4a_n ^3 −3a_n ; ∀n≥1)) :} a_n =? |

|
| A. lim_(x→+∞) Σ_(k=1) ^n [tan((kπ)/(2n))] |