Question and Answers Forum

All Questions Topic List

OthersQuestion and Answers: Page 56

Question Number 114682 Answers: 1 Comments: 0

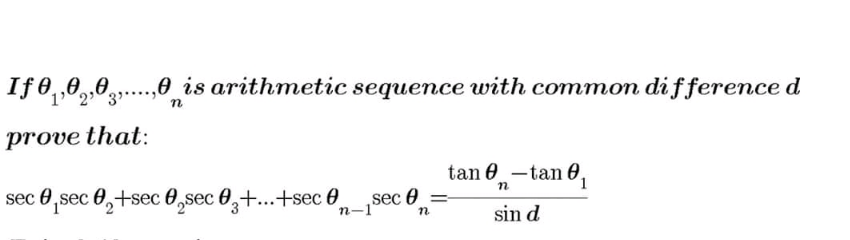
Question Number 114615 Answers: 1 Comments: 0

Question Number 114561 Answers: 1 Comments: 0

Question Number 114433 Answers: 1 Comments: 0

find sum of the series 1^2 −3^2 +5^2 −7^2 +9^2 −11^2 +...+(4n−3)^2 −(4n−1)^2

$f i n d s u m o f t h e s e r i e s$ $1^{2} - 3^{2} + 5^{2} - 7^{2} + 9^{2} - 11^{2} + . . . + {(4 n - 3)}^{2} - {(4 n - 1)}^{2}$

Question Number 114343 Answers: 0 Comments: 4

How many ways can we place 5 identical books and another 6 identical books on a shelf?

$How many ways can we place 5 identical$ $books and another 6 identical books$ $on a shelf ?$

Question Number 114032 Answers: 0 Comments: 0

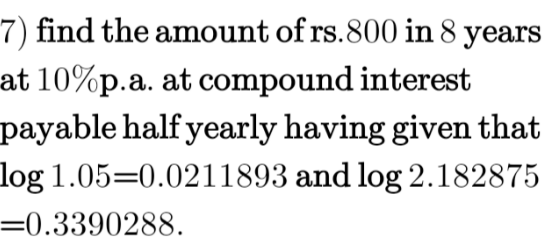
Question Number 113897 Answers: 1 Comments: 0

Question Number 113756 Answers: 2 Comments: 1

∫_0 ^1 ((log(x+1))/x)dx

$\int_{0}^{1} \frac{l o g (x + 1)}{x} d x$

Question Number 113637 Answers: 0 Comments: 0

Montrer que pour 0<z<1 on a Γ(z)Γ(1−z)=(π/(sin(πz)))

$M o n t r e r q u e p o u r 0 < z < 1 o n a$ $Γ (z) Γ (1 - z) = \frac{π}{s i n (π z)}$

Question Number 113499 Answers: 0 Comments: 0

Question Number 113490 Answers: 0 Comments: 1

Question Number 113456 Answers: 0 Comments: 0

Question Number 113455 Answers: 1 Comments: 1

Question Number 113354 Answers: 0 Comments: 3

( ((n),(0) )/2)−( ((n),(1) )/3)+( ((n),(2) )/4)−( ((n),(3) )/5)+.....n

$\frac{(\begin{matrix} n \\ 0 \end{matrix})}{2} - \frac{(\begin{matrix} n \\ 1 \end{matrix})}{3} + \frac{(\begin{matrix} n \\ 2 \end{matrix})}{4} - \frac{(\begin{matrix} n \\ 3 \end{matrix})}{5} + . . . . . n$

Question Number 113336 Answers: 0 Comments: 0

If 1, a^2 ,a^3 ,...,a^(n−1) are the roots nth of unity , prove that : (1+a)(1+a^2 )(1+a^3 )...(1+a^(n−1) ) = n−2⌊(n/2)⌋

$I f 1, a^{2}, a^{3}, . . ., a^{n - 1} a r e t h e r o o t s$ $n t h o f u n i t y,$ $p r o v e t h a t : (1 + a) (1 + a^{2}) (1 + a^{3}) . . . (1 + a^{n - 1})$ $= n - 2 ⌊ \frac{n}{2} ⌋$

Question Number 113190 Answers: 1 Comments: 3

∫_0 ^1 ((logx)/(x−1))dx

$\int_{0}^{1} \frac{l o g x}{x - 1} d x$

Question Number 113185 Answers: 1 Comments: 0

Question Number 112838 Answers: 1 Comments: 0

What is the sum of all the solutions of the equation ∣2x+8∣^2 −∣9x+36∣−9=0

$What is the sum of all the solutions$ $of the equation ∣ 2 x + 8 ∣^{2} - ∣ 9 x + 36 ∣ - 9 = 0$

Question Number 112809 Answers: 1 Comments: 0

Question Number 112707 Answers: 0 Comments: 0

Question Number 112454 Answers: 1 Comments: 1

(1) find the locus ∣z−z_1 ∣ = 2 meets the positive real axis (2)On a single Argand diagram, sketch the loci → { ((∣z−z_1 ∣=2)),((arg(z−z_2 )=(π/4))) :}

$(1) find the locus ∣ z - z_{1} ∣ = 2 meets$ $the positive real axis$ $(2) On a single Argand diagram, sketch$ $the loci \to {\begin{cases} ∣ z - z_{1} ∣= 2 \\ \arg (z - z_{2}) = \frac{π}{4} \end{cases}$

Question Number 112430 Answers: 0 Comments: 0

Π_(n=1) ^∞ (1/(1−x^n ))

$\underset{n = 1}{\prod^{\infty}} \frac{1}{1 - x^{n}}$

Question Number 112245 Answers: 0 Comments: 0

(1/(1+x^2 ))+(1/(1+x^4 ))+(1/(1+x^8 ))+..... ( x>1)

$\frac{1}{1 + x^{2}} + \frac{1}{1 + x^{4}} + \frac{1}{1 + x^{8}} + . . . . . (x > 1)$

Question Number 112162 Answers: 1 Comments: 3

Question Number 111975 Answers: 1 Comments: 0

Question Number 111957 Answers: 0 Comments: 31

“MATHEMATICS” CONTAINS ALL THE LETTERS OF “ETHICS”. IS THERE ANY LESSON FOR US IN ABOVE SAYING? FOR “math-lovers”? FOR “math-giants”? FOR “overflow-mathematicians”? ........ ...... _( BTW this saying belongs to me)

$‘ ‘ {MATHEMATICS}^{″}$ $CONTAINS$ $ALL THE LETTERS OF$ $‘ ‘ {ETHICS}^{″} .$ $IS THERE ANY LESSON FOR US$ $IN ABOVE SAYING ?$ $F O R ‘ ‘ m a t h - {l o v e r s}^{″} ?$ $F O R ‘ ‘ m a t h - {g i a n t s}^{″} ?$ $F O R ‘ ‘ o v e r f l o w - {m a t h e m a t i c i a n s}^{″} ?$ $. . . . . . . .$ $. . . . . .$ $_{B T W t h i s s a y i n g b e l o n g s t o m e}$

Pg 51 Pg 52 Pg 53 Pg 54 Pg 55 Pg 56 Pg 57 Pg 58 Pg 59 Pg 60

Contact: info@tinkutara.com