
Question and Answers Forum
OthersQuestion and Answers: Page 60


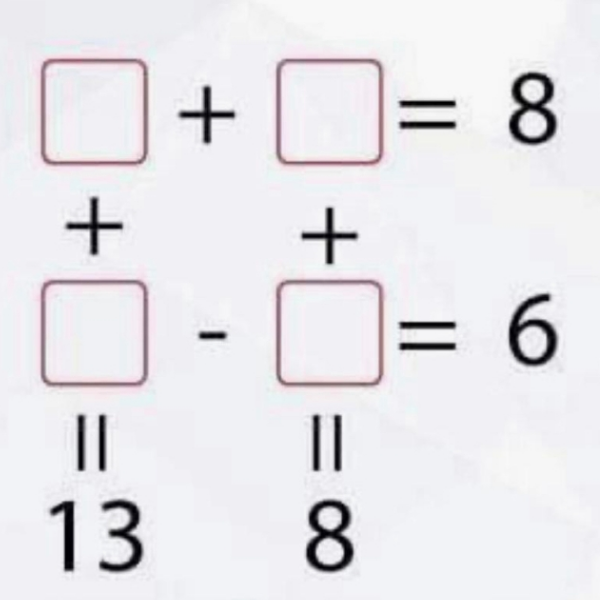



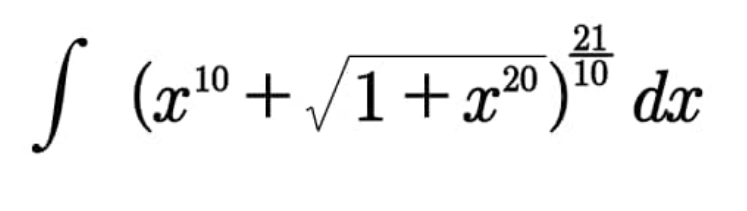


|
Question and Answers Forum |
OthersQuestion and Answers: Page 60 |

|

|
| if y^((n)) is the derivative of the function y of the order n, then ∫y^((n)) dx =........ |
| find (d^n y/dx^n ) for f(x)^ =(1/(√(1−x))) |

|
| ((1/8)÷(1/8))((1/7)÷(1/7))((2/3)÷(2/3))= ? |

|
| find : lim_(x→1) (((x+2)^2 +(x+1)^3 −17)/((√(x+3))−((x+7))^(1/3) )) |

|
| Σ_(n=1) ^∞ ((e^n n!)/n^n ) |
| Evaluate (1/2) + (3/8) + (3/(16)) + (5/(64)) + ..... |
| FUN TIME AGAIN! S_n =1+2+3+4+5+6+7+8+9+.. S_n =1+(2+3+4)+(5+6+7)+... S_n =1+9+18+27+... S_n =1+9(1+2+3+4+5+6+7.......) S_n =1+9S_n S_n =−(1/8) S_n =1−1+1−1+1−1+1−1+1−1+.. S=(1/2) S_n =1−2+4−8+16−32+..... S_n =(1/(1+2))=(1/3) S_n =1+2+4+8+16+... S_n =1+2(1+2+4+8+...) S_n =1+2(1+2(1+2+4+8+...) S_n =1+2(1+2S_n ) −3S_n =3⇒S_n =−1 |

|
| solve for real values of x the equation 4(3^(2x+1) )+17(3^x )=7. if m and n are positive real numbers other than 1, show that the log_n m+log_(1/m) n=0 |
| Π_(n=1) ^∞ ((n/(n+1)))^2 |
| For fun! S_n =1+2+3+4+5+6+7+... 2S_n = 2 + 4 + 6 +.. −S_n =1+3+5+7+9+11+..... −(−(1/(12)))=1+3+5+7+9+11+... 1+3+5+7+9+....=(1/(12)) S_n =1+2+3+4+5+6+7+.... S_n =1+(1+1)+(1+2)+(1+3)+... S_n =(1+1+1+....)+S_n 1+1+1+1+1+1+....=0 |
| if i^( 5n +1 ) = 1 , n∈Z then show that : n = 3+4p ,p∈Z |
| Σ_(n=1) ^∞ (((n/(n+1)))^2 −(2/(n+1))−1) |
| muhun kitu pisan |
| prove that : a) ∫_(−3) ^(−1) x^2 dx ≥∫_1 ^3 (2x−1)dx b)∫_(−2) ^0 xdx ≤∫_0 ^2 (x^2 + x )dx c)∫_1 ^4 (x^2 + 2)dx ≥∫_2 ^5 (2x −5)dx d)∫_(−π) ^(−((3π)/4)) cos 2x dx ≥∫_((3π)/4) ^π sin 2x dx |
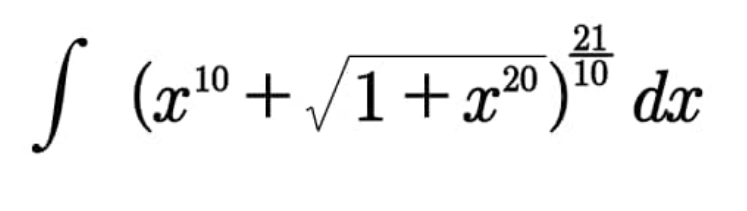
|

|

|
| Solve : 3^x = 4x |
| e^e^(e.....∞) =? |
| 1+1+1+1+1+1+1+....=S_n S_n =1+1+1+1+1+1+1+.... 2S_n = 2 + 2 + 2+....... .......... subtracting −S_n =1−1+1−1+1−1+1−1+1−1+.... −S_n =(1/2) S_n =−(1/2) I have found this while experiment . I know the sum diverges but is it pretty cool? Kindly rectify me if there is any fault on this non rigorous process I have found some Ramanujan proof S_n =1+2+3+4+5+6+7+... 4S_n = 4+ 8 + 12+... −3S_n =1−2+3−4+5−6+7−8+...... −3S_n =(1/4) S_n =−(1/(12)) Ramanujan had done this on his notebook |