
Question and Answers Forum
OthersQuestion and Answers: Page 61








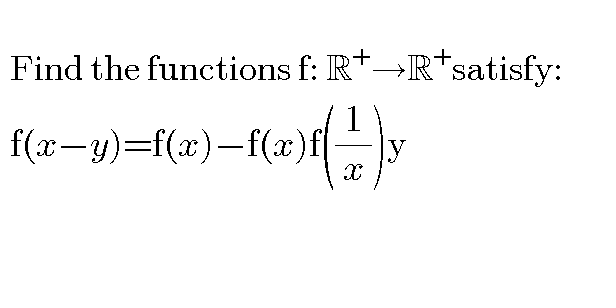
|
Question and Answers Forum |
OthersQuestion and Answers: Page 61 |

|
| ∫((log(((1+(√5))/2)(√x)−1))/(x^(√x) log(((1+(√5))/2)(√x)+1)−1)) |

|
| solve : y^2 + x^2 = −sin(θ) ., (π/2)≥ θ≥−(π/2) |
| Σ_(n=1) ^∞ ((n!)/n^n ) |
| 1−1+1−1+1−1+1−1+.....=(1/2) {But it diverges 1+1+1+1+1+1+1+......=−(1/2) {But it diverges 1+2+4+8+16+.....=−1 {But it diverges 1+2+3+4+5+6+7=−(1/(12)) {But it diverges 1−2+4−8+.....=(1/3) {But it diverges 1−2+3−4+5−6+.....=(1/4) {Is it a divergent????? |
| Evaluate: ∫((sin x)/x)dx |
| Σ_(r=1) ^∞ i^r +Σ_(r=0) ^∞ i^r |
| 2x=5 x=? −−− for test app only |
| 12+14+24+58+164....upto nth terms |

|
| show that: cosθ + cos2θ + ....cos nθ= ((cos (1/2)(n +1)θ sin(1/2)nθ)/(sin (1/2)nθ)) Show that: sin θ + sin 2θ + ....+ sin nθ = ((sin (1/2)(n + 1)θ sin(1/2)nθ)/(sin (1/2)nθ)) where θ ∈ R and θ ≠2πk , k ∈Z |

|

|

|
| 2+3.3+4.3^2 +5.3^2 +.....up to n terms |

|

|
| Sir MJS & Sir John Santu You both have decided to leave this forum for different reasons. Being agree with your reasons and accepting your right of decision I dare to suggest not to disconnect fully from the forum.Please stay connected although for very short time on daily/weekly basis.This is also necessary because we have no means to contact you. After all this is only a request. You may or may not accept it. |
| please how calculate the development limity of f(x,y)=x^y ,take a( 3,2) at order one and two |
| if f(x)≤2l +1 and ∫_1 ^3 f(x)dx≤l^2 find the value of l |
| A four-sidex dice with numbered 1, 2, 3, and 4 is thrown and the number at the base is read. The dice is biased such that the probabilies P_1 , P_2 , P_3 , and P_4 to obtain 1, 2, 3, and 4 respectively are in an arithmetic progression. 1\ Given P_4 =0.4, calculate P_1 , P_2 , and P_3 . 2\ The dice is thrown n-times (n≥1). The throws are assumed to be independent, 2 by 2, and identical. Given U_n -the probability of obtaining for the first time the fourth-n^(th) throw; a\Express U_n in terms of n= b\Given S_n =Σ_(i=1) ^n U_i i. Express Sn in terms of n, and find its limit. ii. Determine the smallest natural number such that S_n >0.999 |
| The Gamma function Γ(α) is defined as follows; Γ(α)=∫_0 ^∞ y^(α−1) e^(−y) dy , α>0 a\ Show that Γ(α+1)=αΓ(α). b\Conclude that Γ(n)=(n−1)! , n=1, 2, 3, ... c\Determine Γ(55). |
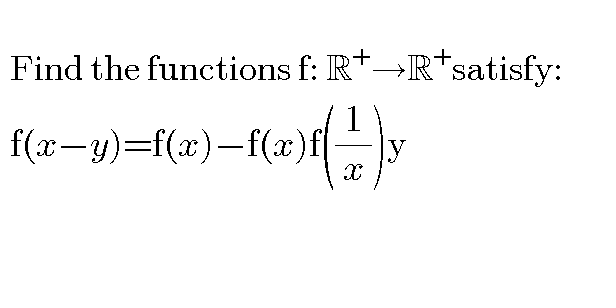
|
| A random variable, X, has a Gamma distribution with parameters α and β, (α, β>0). The p.d.f has the form f(x)=(1/(Γ(α)β^α ))x^(n−1) e^(−x/β) , for x>0 , Γ(α)=(1/β^α )∫_0 ^∞ x^(α−1) e^(−x) dx a\ Show that the Gamma density is a proper p.d.f. b\Find the mean, variance, and moment-generating function of the Gamma distribution. c\Find the fourth moment using the definition of moments. |
| A car is currently valued at $70350.00. If it loses 12% of its value at the beginning of each year, a) find its value after three and half years. b) find the depreciation after three years |