
Question and Answers Forum
OthersQuestion and Answers: Page 83



|
Question and Answers Forum |
OthersQuestion and Answers: Page 83 |
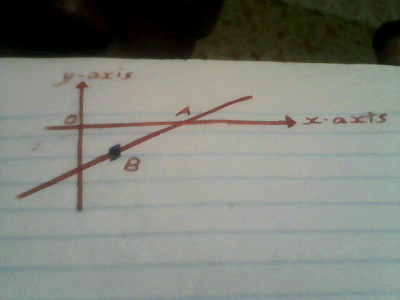
| solve the system of equations { ((3∣x−5∣+4=y)),((∣y−3∣=4x−12)) :} |
| ⋓si⋒g ChineseRemainderTheorm ∂etermine polynomial p(x) such that p(x)≡8(mod x+1) p(x)≡−24(mod x+3) p(x)≡6(mod x) p(x)≡0(mod x+2) |
| A relation R defined by _((x,y)) R_((u,v)) ⇔ v^2 −y^2 = u^2 −x^2 show that R is an equivalent Relation. |
| find the range of values of ∣((x^2 −9)/3_ )∣= ((9−x^2 )/3) |
| given that the roots of the equation 4x^2 + 6x + 9 =0 are λ and δ where λ = (1 + α^2 +β^2 ) and δ = α^3 + β^3 find an equation whose roots are (1/(αλ)) and (1/(βδ)) |
| given the function f(x) = { ((x^2 , for 0≤ x< 2)),((ax + 3, for 2≤ x < 4)) :} is periodic of period 4, and is continuous. a) Find the value of a. b) Find the valu of f(6) c) sketch the graph for y =f(x). help me please, for the graph i don′t know wbere to put y=x^2 and y = ax + 3 and where do i put a closed dot and an open dot. |
| show that ∃ n ∈ N^(+ ) : sin^n x + cos^n x = 1 and cosh^n x − sinh^n x = 1. Hint: use Induction method. |
| please explain the fact that ∫(1/x)dx = ln x + k |
| Help me obtain the value of e from (1 + (1/n))^n how do i go about it. |
| Can you please tell me, where does this formula come from? And what means the factorial of a non- integer number? π = ((1/2)!)^2 × 4 I′ve verified the above equation with calculator. Thank you |
| I have tried to solve Q#67299 Please see and give critical remarks |
| Evaluate:∫(√(x(√(x+1)))) dx |
| dear scientist. i did some research on the energy obtained from the sun any other source by a liquid, of density ρ , velocity v, viscosity η and distance travelled d. i came out with the equation E = k ( vρ η^3 d^2 ) where k is a costant i still need to determine from more experiment. But please i want you guys great people to check if the equation is in confirmity and if atall it is correct so i can do some changes. thanks in advanced dear scientist. |
| G(x)= (x+1)(x+3)Q(x) + px +q a) Given that G(x) leaves a remainder of 8 and −24 when divided by (x+1) and (x+3) respectively,find the remainder when G(x) is divided by (x+1)(x+3). b) Given that x+2 is a factor of G(x) and that the graph of G(x) passes through the point with coordinates (0,6) find G(x) |
| Find the third degree polynomial which vanishes when x =−1 and x = 2, which has a value 8 when x =0 and leaves a remainder ((16)/3) when divided by 3x + 2. |
| explicitez la suite u_n definie par la relation; { ((u_0 =0, u_1 =1)),((u_(n+2) =u_(n+1) +u_n ∀n∈∤N)) :} u_n =???????? −calculer la lim _(n→∞) (u_(n+1) /u_n )=??? −montre que Σ_(k=0) ^n u_k =u_(n+2) −1 voila^′ |

|

|

|
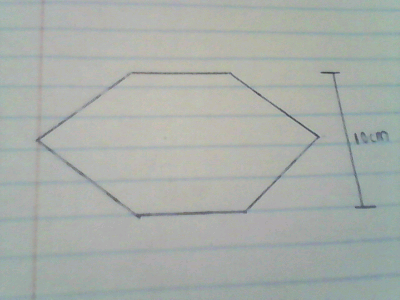
| The external length,width and height of an open rectangular container are 41cm,21cm and 15.5cm respectively. The thickness of the material making the container is 5mm.If the container has 8litres of water,calculate the internal height above the water level. Ans:5cm |
| which of the sequences converges ? 1) a_n = n−(1/n) 2) a_n = ((−1)^n +1)(((n+1)/n)) |
| A and B are two towns 360km apart. An express bus departs from A at 8a.m and maintains an average speed of 90km/h between A and B. Another bus starts from B also at 8a.m and moves towards A making four stops at four equally spaced points between B and A. Each stop is of duration 5 minutes and the average speed between any two stops is 60km/h. Calculate the distance between the two buses at 10p.m. |
| A town N is 340km due west of town G and town K is due west of town N. A helicopter Zebra left G for K at 9a.m. Another helicopter Buffalo left N for K at 11a.m. Helicopter Buffalo travelled at an average speed of 20km/h faster than helicopter Zebra. If both helicopters reached K at 12.30p.m, find the speed of helicopter Buffalo. |
| Two towns T and S are 300 km apart. Two buses A and B started from T at the same time travelling towards S. Bus B, travelling at an average speed of 10km/h greater than that of A reached S 1(1/4) hours earlier. (a) Find the average speed of A (b) How far was A from T when B reached S. |

|

|