
Question and Answers Forum
Permutation and CombinationQuestion and Answers: Page 10


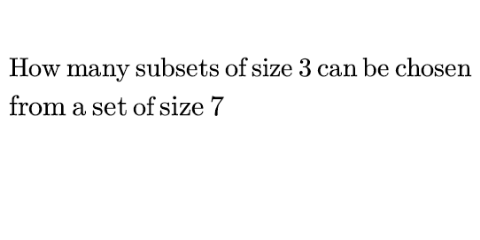


|
Question and Answers Forum |
Permutation and CombinationQuestion and Answers: Page 10 |
| Show that: ^n C_r =((Π_(k=0) ^(r−1) n−k)/(r!)) |
| It is required to seat 5 men and 4 women in a row so that the women occupy the even place. How many such arrangements are possible ? |
| use error fxn use polar coordinates to find ∫e^(−x^2 ) dx |
| it is a known that a particular machine will make product with a qualified rate of 90% when it is running well, but will do so with a qualified rate of only 30% when it is not running well. The probability that machine is running well is 75% normally . Suppose that one day the first product made by the machine is qualified. Find the probabiliy that the machine is running well at this time. |
| What is the coefficient x^(10) in the expansion of (1+x^2 −x^3 )^8 |

|

|
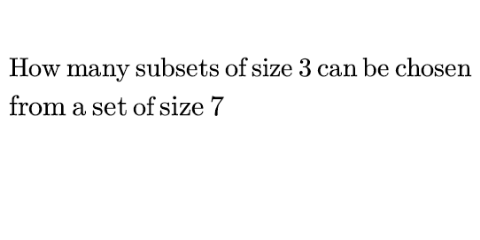
|
| three subject group are to be formed randomly by 15 students (including 3 girls) under the condition that each groups consist 5 students and each student attends only one group. flnd the probabilities that of the following events (1) there is exactly one girl in each group (2) the 3 girls attend the same group |
|
| determinant (((old plate : EEU 874)),((new plate : 1BXK 267))) Old California license plate consisted of a sequence of three letters followed by three digits (see figure above). Assuming that any sequence of letters and digits was allowed (though actually some combinations of letters were disallowed), how many license plate were available ? |
| Eight eligible bachelor and seven beautiful models happen randomly to have purchased single seats in the same 15−seats row of theather. On the average , how many pairs of adjacent seats are ticketed for marriageable couples ? |
| If α and β are the coefficient of x^8 and x^(−24) respectively in the expansion of [ x^4 +2+(1/x^4 ) ]^(10) in powers of x then (α/β) is equal to |
| Five children sitting one behind the other in a five seater merry−go−round ,decide to switch seats so that each child has new companion in front. In how many ways can this be done? |
| There are 20 persons at a party. Maria dansed with 7 boys, Stacy dansed with 8 boys, Monia dansed with 9 boys and Eve dansed with all the boys at the party. How many girls are there at the party ? |
| How many password containing 6 characters of the letters in the word ′′ Move Now ′′ ? |
| Mr. Rahmat decided to create a password with the form numbers and letterse intermittntly intermittent ( can also be letters and numbers intermittently) but no nmbers and letters are the same. It chooses to use numbers on the set {2, 5, 8, 9} and selects the letters on the set { A, X, Y, W,Z} How many passwords can I create |

|

|
| How many words with at least 2 letters can be formed from UNUSUALNESS? |
| How many integers between 999 and 4000 (both are included) can be formed using digits 0,1,2,3,4 if repetition of digits is allowed? |
| How many 4 letters word can be formed from COMMUNICATION |
| How many four−digit numbers between 2000 and 4000 can be formed from the numbers 0, 1, 2, 3, 4 and 5 if repitition is allowed? |
| In a room containing N people N>3, at least one person has not shaken hands with everyone else in the room. What is the maximum number of people in the room that could have shaken hands with everyone else? |
| There are 12 students in a party. Five of them are girls. In how many ways can these 12 students be arranged in a row if (i) there are no restrictions? (ii) the 5 girls must be together (forming a block)? (iii) no 2 girls are adjacent (iv) between two particular boys A and B , there no boys but exactly 3 girls? |
| Find the number of ways to choose a pair {a,b} of distinct numbers from the set {1,2,3,...,50} such that (i) ∣a−b∣ = 5 (ii) ∣a−b∣ ≤ 5 |