
Question and Answers Forum
Permutation and CombinationQuestion and Answers: Page 12

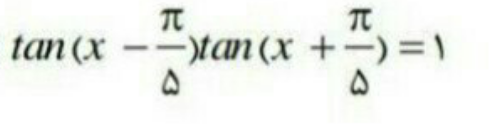


|
Question and Answers Forum |
Permutation and CombinationQuestion and Answers: Page 12 |

|
| Π_(k=1) ^∞ cos((x/2^k )) = ? |
| Find the number of possible arrangements of the letters in the word PENCILS if (a) ′E′ is next to ′I′ (b) E comes before I (c) there are three letters between E and I |
| we have 15 different mathematics books, 10 different physics books and 12 different chemistry books. we should choose 6 books such that they contain all three kinds of books. in how many ways can we do this? |
| Suppose once more we′re asked to choose four students from high school class of 15 to form a committee but this time we have a restriction : we don′t want to committee to consist of all seniors or all juniors .suppose there are eight seniors and seven juniors in the class. How many different committe can we form? |
| In how many ways can the letters of the word LEVITATE be arranged if the vowels must not be next to each other |
| How many sets of 3 numbers each can be formed from the numbers { 1,2,3,...,20 } if no two consecutive numbers are to be in a set ? |

|
| (1) solve the equation ((x−49)/(50)) + ((x−50)/(49)) = ((49)/(x−50)) + ((50)/(x−49)) (2) How many numbers from 12 to 12345 inclusive have digits which are consecutive an in increasing order, reading from left to right ? |
| Find the number of all 5 digit numbers x_1 x_2 x_3 x_4 x_5 with x_1 ≥x_2 ≥x_3 ≥x_4 ≥x_5 . |
| In how many different ways can we select 5 numbers from 9 numbers {1,2,3,...,9}? A number may be selected more than one time. |
| Assuming you have enough coins of 1,5,10,25,and 50cents. In how many ways can you make a change for 1dollar. |
| Find the number m of ways to partition 10 students into four team so that two team contains 3 students and two team contains 2 students . |
| Find the number m of non negative integer solution of x+y+z=18 |
| The number 1,2,3,4,...,7 are randomly divided into two non −empty subsets. The probability that the sum of the numbers in the two subsets being equal is (r/s) expressed in the lowest term. Find r+s ? |
| A five digits number divisible by 3 is to be formed using the number 0,1,2,3,4 and 5 without repetition The total number of ways this can be done is __ |
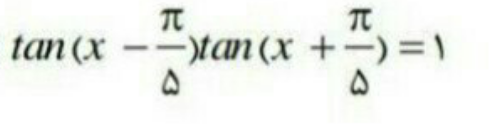
|

|
| The secret number is made from the numbers 1,2,2,3,3,4,5. Many secret numbers can be created if the same number is not adjacent except in the first two place is _ (a)1142 (b) 1212 (c) 1246 (d) 1248 (e) 1250 |
| There are 3 teachers and 6 students who will sit on the 9 available seats. many arrangements they sit if each teacher is flanked by 2 students |
| how many 6 digit numbers exist which are divisible by 11 and have no repeating digits? |

|
| 2 women and 4 men will sit on the 8 available seats and surround the round table . The many possible arrangements of them sitting if they sat randomly |
| (1)Given ((P _(n−1)^(2n+1) )/(P _n^(2n−1) )) = (3/5) , find n = ? (2) in how many ways can 6 persons stand in a queue? (3) how many different 4 letter words can be formed by using letters of EDUCATION using each letter at most once ? |
| There are 6 people going to sit in a circle . The number of arrangements they sit if there are 2 people who always sit next to each other |
| you have 2 identical mathematics books, 2 identical physics books, 2 identical chemistry books, 2 identical biology books and 2 geography books. in how many ways can you compile these books such that same books are not mutually adjacent? |