
Question and Answers Forum
Permutation and CombinationQuestion and Answers: Page 13
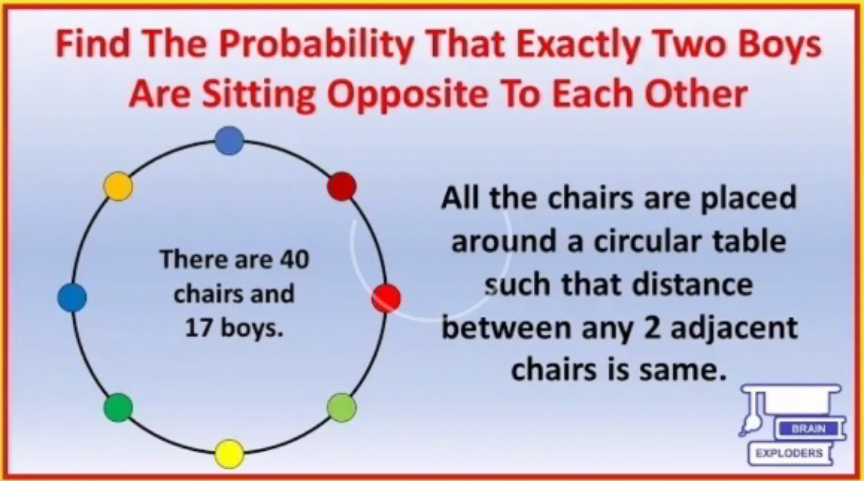



|
Question and Answers Forum |
Permutation and CombinationQuestion and Answers: Page 13 |

|
| A rectangular cardboard is 8cm long and 6cm wide. What is the least number of beads you can arrange on the board such that there are at least two of the beads that are less than (√(10))cm apart. |
| What is the maximum number of points to be distributed within a 3×6 to ensure that there are no two points whose distance apart is less than (√2)? |
| There are 4 identical mathematics books, 3 identical physics books, 2 identical chemistry books. in how many ways can you compile the 9 books such that same books are not mutually adjacent. |
| There are 4 identical mathematics books, 2 identical physics books, 2 identical chemistry books and 2 identical biology books. in how many ways can you compile the 10 books such that same books are not mutually adjacent. |

|
| Σ_(n=1 ) ^(11) (((−1)^(n+1) (4n+2))/(4n(n+1))) please help |

|
| Find the minimum number of n integers to be selected from S={1,2,3,...11} so that the difference of two of the n integers is 7. |

|
| A rectangular cardboard is 8cm long and 6cm wide. What is the least number of beads you can arrange on the board such that there are at least two of the beads that are less than (√(10))cm apart. |
| A blind man is to place 5 letters into 5 pigeon holes, how many ways can 4 of the letters be wrongly placed? (note that only one letter must be in a pigeon hole) |
| There are 2016 straight lines drawn on a board such that (1/2) of the lines are parallel to one another. (3/8) of them meet at a point and each of the remaining ones intersect with all other lines on the board. Determine the total number of intersections possible. |
| What is the maximum number of points to be distributed within a 3×6 to ensure that there are no two points whose distance apart is less than (√2)? |
| What is the sum of the coefficients in the expansion of (2015v−2015u+1)^(2015) ? |
| A teacher conducts a test for five students. He provides the marking scheme and asked them to exchange their scripts such that none of them marks his own script. How many ways can the students carry out the marking? |
| Tricolours flags(each flag having three different strips of non−overlapping colours) are to be designed using white,blue,red,yellow and black strips. How many of the flags have blue colour? |
| In a tennis tournament n women and 2n men played. Each player played exactly one match with every other player. If there are no ties and the number of the matches won by women to the number of matches won by men is 7:5, find n. |
| How many ways can the letters in the word MATHEMATICS be rearranged such that the word formed neither starts nor ends with a vowel, and any four consecutive letters must contain at least a vowel? |
| A blind man is to place 6 letters into 6 pigeon holes, how many ways can atleast 5 letters be wrongly placed? (Note that only one letter must be in a pigeon hole). |
| In the square PQRS, K is the midpoint of PQ, L is the midpoint of QR, M is the midpoint RS, N is the midpoint of SP and O is the midpoint of KM. A line segment is drawn from each pair of points from (K,L,M,N,O,P,Q,R,S). These line segments create points of intersections not contained in (K,L,M,N,O,P,Q,R,S). How many distinct such points are there? |
| How many ways can the letters in the word MATHEMATICS be rearranged such that the word formed either starts or ends with a vowel, and any three consecutive letters must contain a vowel? |
| How many are the permutations of 1 − a little rubik′s cube with 4 squares by side 2 − a classical one with 9 squares by side |
| SUCCESSFULLY How many different words can you form using these letters so that no two same letters are adjacent? |
| ((bemath)/★) prove that (((n−1)),(( r)) ) + (((n−1)),((r−1)) ) = ((n),(r) ) |
| ((BeMath)/(⊂⊃)) (1)find ((1/2))! (2)∫_0 ^(π/2) ((x sin x)/((1+cos x)^2 )) dx |