
Question and Answers Forum
Permutation and CombinationQuestion and Answers: Page 21



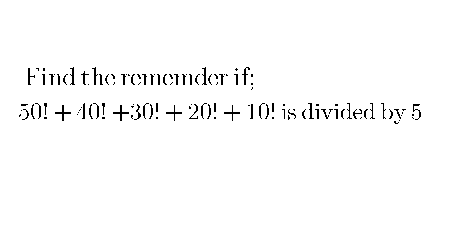



|
Question and Answers Forum |
Permutation and CombinationQuestion and Answers: Page 21 |
| Prove that Σ_(r=0) ^n r ((n),(r) )^2 = n (((2n − 1)),(( n − 1)) ) |
| Consider triangle ABC.If 206 lines are drawn from A to BC how many triangles are formed? |
| A panel of 3 women and 4 men is to be formed from 8 women and 7 men.Find the number of ways which the panel can be formed if it must contain at least 2 women. |
| Three boys,two girls and a puppy sit at a round table.In how many ways can they be arranged if the puppy is to be seated i)between the two girls ii)between any two boys |

|

|

|
| In how many ways can a committee of 11 people be selected from 9 people. |
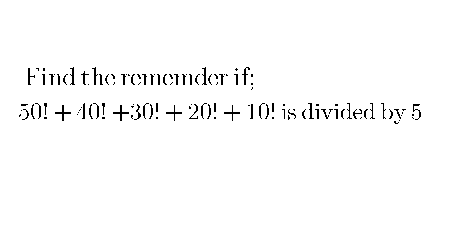
|
| A committee of 4 is to be formed from 4 principals and 5 students.In how many ways can this be done if a particular student and a principal must be in the committee. |
| show that C_(n−1) ^(n+r−1) =C_r ^(n+r−1) |
| 4 couples are to take a photograph with a newly wedded couple in a wedding party.In how many ways can this be done if: i)the celebrated couple must stand in the middle ii)each couple must stand next to each other iii)the celebrated couple must not stand next to each other |
| Prove that (((n^2 )!)/((n!)^(n+1) )) is always an integer for n∈N. |

|
| algebra1ic |
| Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour. |
| Prove that Σ_1 ^(n−2) k ((( n−2)),(( k)) ) (((n+2)),((k+2)) ) = (n−2) (((2n−1)),((n−1)) ) |
| Given n ∈ N prove that Σ_(k=1) ^n k(n+1−k)= ((( n+2)),(( 3)) ) |

|
| The president of a republic wishes to assign the premiership,the vice-premiership,and six other cabinet posts to a selected group of 8,comprising of 6 career diplomats and 2 business men.If none of the business men can be made premier or vice premier,in how many ways can the 8 posts be assigned to the 8 people? |
| Using only the integers 4 to 8, how many even numbers can be formed if each must lie between 4000 and 9000? |
| (1) There are 20 boys and 10 girls in a class.If a committee of 6 is to be chosen at random having atleast 2 boys and 2 girls,find the probability that (i) there ara 3 boys in the committee (ii) there are 4 boys in the committee |

|
| (2) Find the 10th trem in the expansion of (2x−(y/2)) |
| (2) Find the middle trem(s) in the expansion of following− (x^2 +(1/x^3 ))^(14) |
| Find the number of all possible different words into which the word INTERFERE can be converted by change of place of letters,if no two consonants must be together. |