
Question and Answers Forum
Permutation and CombinationQuestion and Answers: Page 24

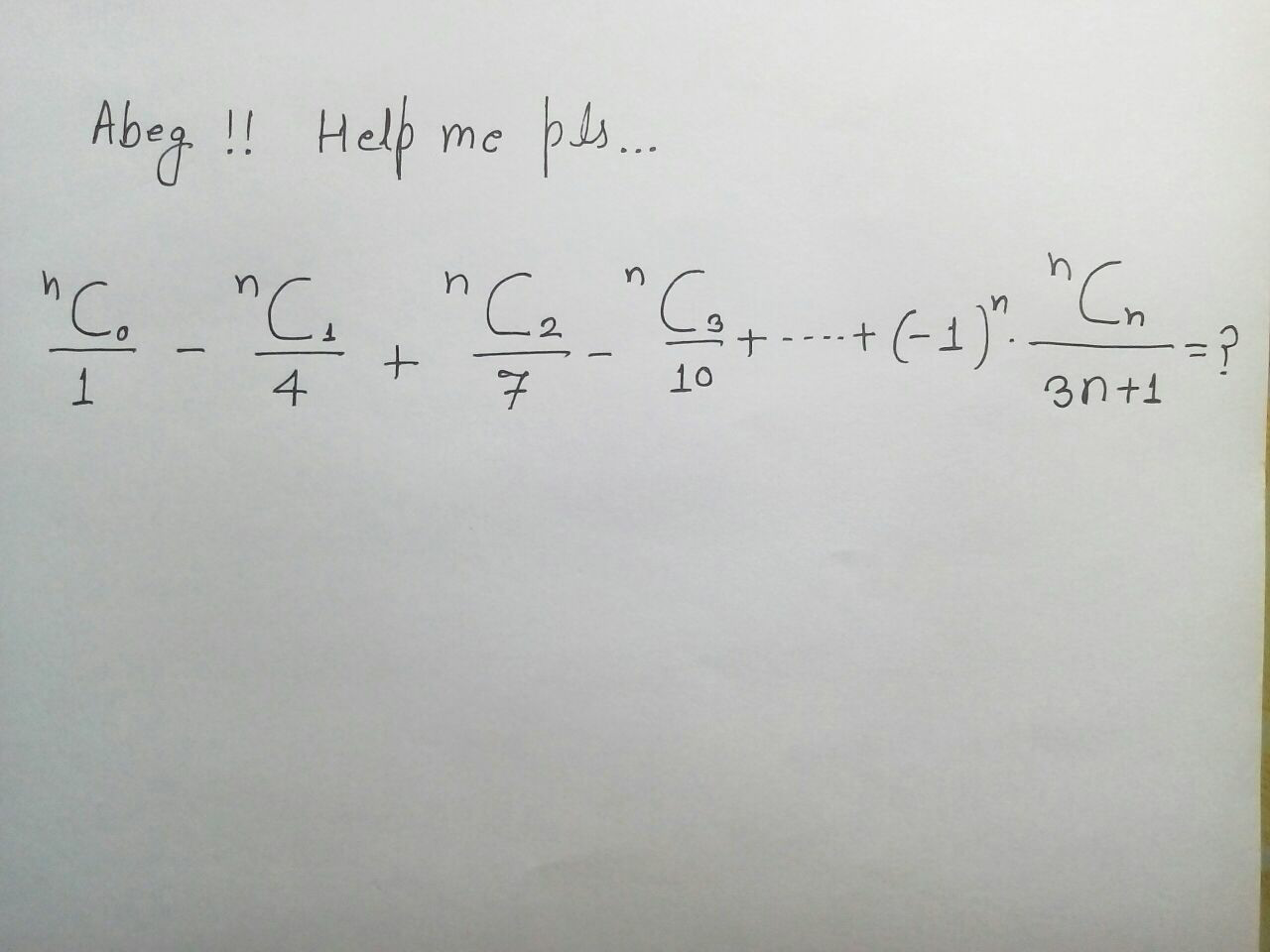

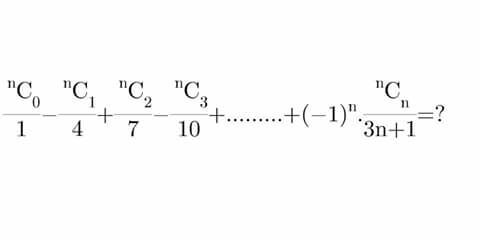



|
Question and Answers Forum |
Permutation and CombinationQuestion and Answers: Page 24 |
| In a basic version of pocker , each players is dealth 5 cards from a standard 52 cards (no pocker). How many diferent 5 cards pocker hand are there ??? |
| 5!! = ? |
| In how many ways can 10 objects be split into two groups containing 4 and 6 objects respectively ? |
| Ten men are present at a club. In how many ways can four be chosen to play bridge if two men refuse to sit at the same table. |

|
| Out of 5 accountants and 7 bankers, a committee consisting of 2 accountants and 3 bankers is to be formed. In how many ways can this be done if (a) Any acountant and any bankers must be included (b) One particular banker must be included (c) 2 accountant cannot be in the committee |
| In how many ways can 24 different articles be divided into groups of 12, 8 and 4 articles respectively |
| The first 3 runners in 100m race were clocked 9.5s, 10s, 10.5s respectively. How far is the first from the third runners when the first runner reached the finished line. |
| Find the coefficient of the term independent of x in the expansion of (((x + 1)/(x^(2/3) − x^(1/3) + 1)) − ((x − 1)/(x − x^(1/2) )))^(10) |
| If n is positive integer prove that the cofficient of x^(2 ) and x^3 in the expansion of (x^2 +2x+2)^n are 2^(n−1) .n^2 and 2^(n−1) n(n−1)(1/3). |
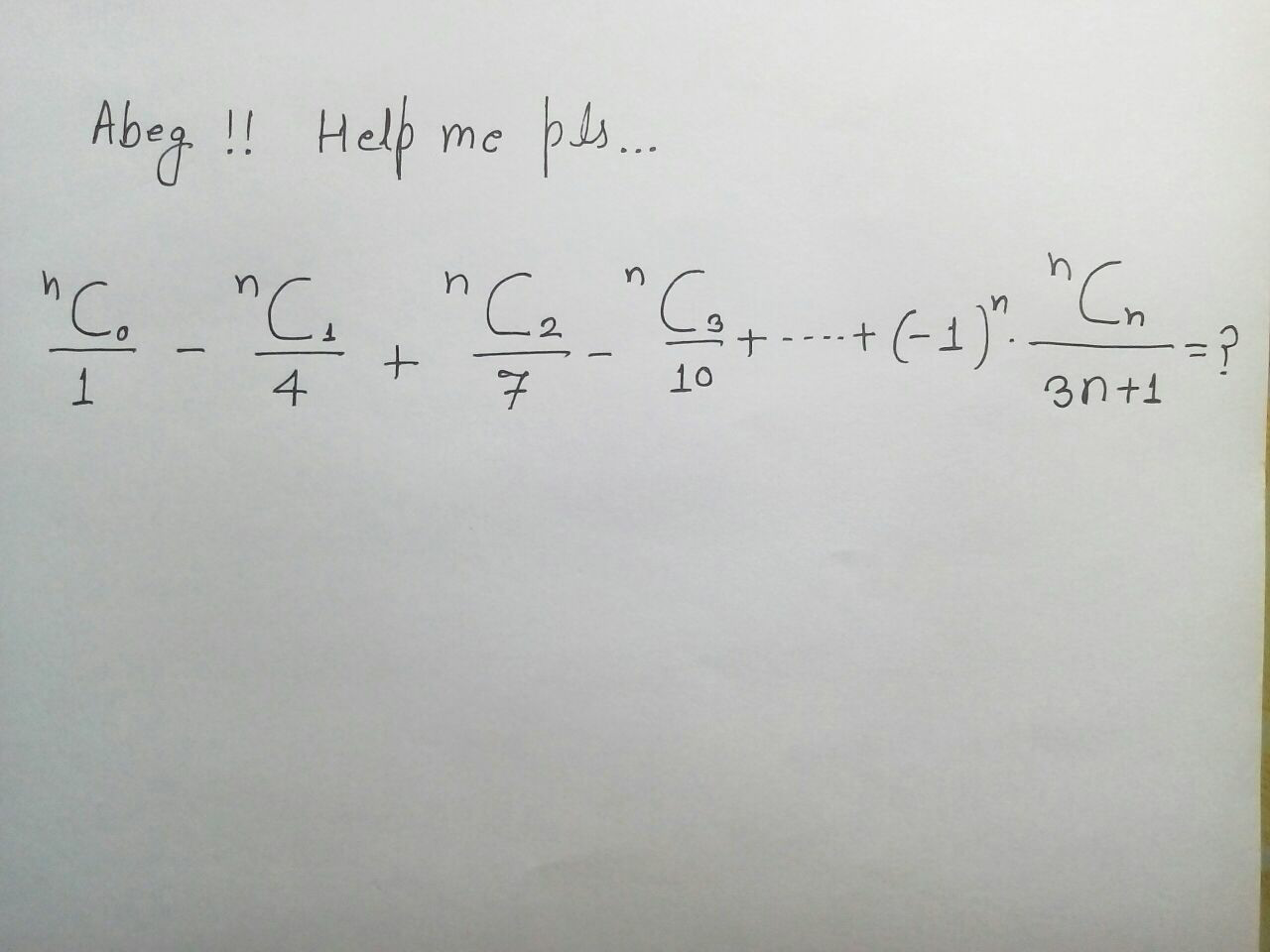
|

|
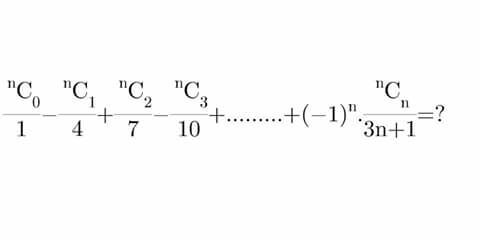
|

|
| Evaluate 10 ×12 × 14 × 16 × 18 × 20 into factorial form |
| 8 |
| If 8C4 = 8Cn . find the value of n |
| A delegation of 4 people is to be selected from 5 women and 6 men. Find the number of possible delegations if (a) there are no restrictions, (b) there is at least 1 woman, (c) there are at least 2 women. One of the men cannot get along with one of the women. Find the number of delegations which include this particular man or woman, but not both. |

|
| Calculate the number of ways in which (a) 5 children can be divided into groups of 2 and 3 , (b) 9 children can be divided into groups of 5 and 4, Hence calculate the number of ways in which 9 children can be divided into groups of 2,3 and 4. |

|
| How many distinct ways are there for a knight to reach from bottom left corner of chessboard to top right corner. (knight going from square a1 to h8). |
| Prove that Σ_(m=1) ^n (((−1)^m ∙(2^m −1) ∙^n C_m )/m) =Σ_(m=1) ^n (((−1)^m )/m) |
| Prove that there are (((n+r−1)),((n−1)) ) ways of placing r identical objects in n compartments, where n>r. |
| Four integers are chosen at random from 0 to 9, inclusive. Find the probability that no more than 2 integers are the same. |
| I have 25 horses and I′d like to know which are the three fastest horses among them. I do not have a clock but I have a race track which can be used by 5 horses at a time. If each horse covers the distance of the track in the same time for every race it runs, find the least number of races that ought to be held in order to identify the three fastest horses. |