
Question and Answers Forum
Permutation and CombinationQuestion and Answers: Page 3



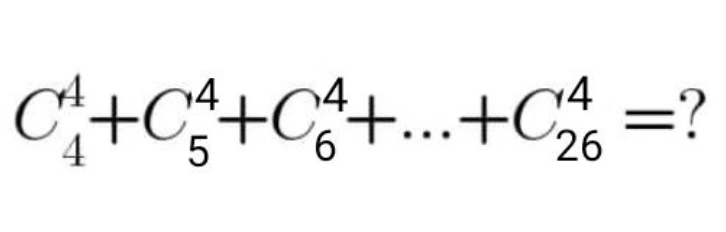
|
Question and Answers Forum |
Permutation and CombinationQuestion and Answers: Page 3 |
| how many different words can be formed from the letters in aaacdefgbbbb such that a “a” and a “b” are not next to each other? (see also Q#195606) |
| Number of distributions of n different articles to r different boxes so as 1)empty box allowed 2)empty box not allowed with proof...kindly help me |

|

|
| Soit x>1. On de^ finie la suite (p_n ) par p_1 =x et ∀n∈IN^∗ p_(n+1) =2p_n ^2 −1 Montrer que lim_(n→+∞) Π_(k=1) ^n (1+(1/p_k ))=(√((x+1)/(x−1))) |
| Prove that ∀n∈IN^∗ Σ_(k=1) ^(2^n −1) (1/(sin^2 (((kπ)/2^(n+1) ))))= ((2^(2n+1) −2)/3) Give in terms of n Σ_(k=1) ^(2^n −1) (1/(sin^4 (((kπ)/2^(n+1) )))) |
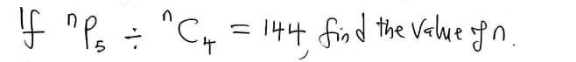
|
| If log_a y = (1/3) and log_8 a = x + 1 then show that y = 2^(x + 1) |
| given f(x)=cx(x−20) and A=(2,5) find the nearst point to A on the graph |

|
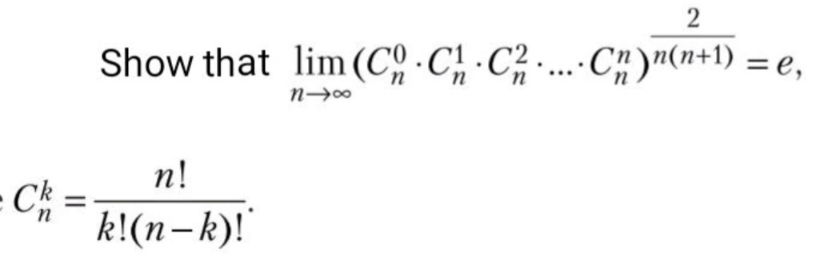
|
| ∫_0 ^( (π/2)) (((sin((x/2^n )))/(sinx))) dx , n ∈ N |
| let S={a,b,c,d,e,f} if we take any subset S (same subset is allowed), it also can be S, which will form S if we join them, order of operation does not matter ({a,b,c,d},{d,e,f}) is the same as ({d,e,f},{a,b,c,d}) how many ways can we choose? |
| how is solution lim_(x→sinπ ) ((sin(π/2))/(sinx))=? |
| f : [1, 3] →R , f(x) = (1/x) A(1, 1) B(1, (1/3)) B′(b, (1/b)) , b ≥ 1 Find i. equation of line AB′ ii. equation of tangent T ′ to C_f at point with x = ((1 + b)/2) iii. Study relative positions of L_(AB ′) , T ′ to C_f |

|
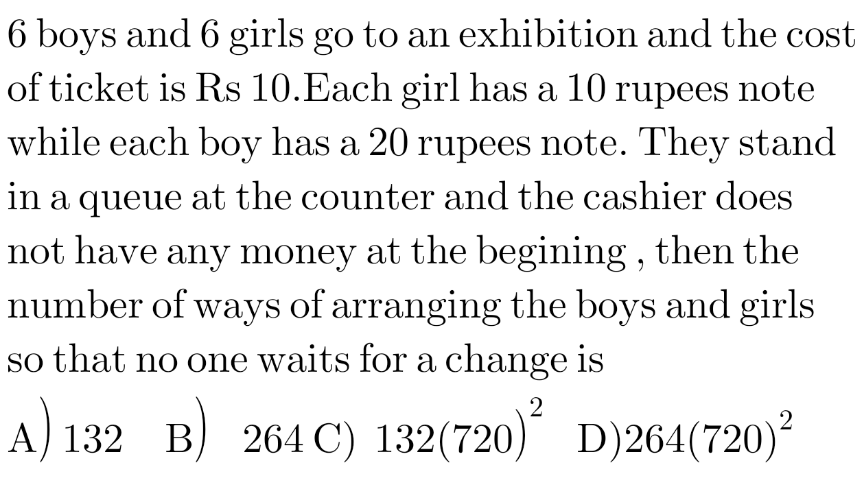
|
| How many non−similar triangles have integer angles in °? |
| you randomly select a 5 digit number. what′s the probability that this number has exactly 3 different digits? |
| find the number of 5 digit natural numbers with strictly ascending digits whose sum is 20. example: 12458 is such a number |
| Find the number of triangles with integer side lengths and perimeter p. |
| Given a set H={1,2,3,...,300. We will a create a subset of H consisting of three elements. If the sum of the three elements is divisible by 3 then the number of subsets that canbe made is x. Find the remainder if x is divided by 100000 |
| prove for r, n ∈ N Σ_(k=r) ^n ((k),(r) ) = (((n+1)),((r+1)) ) (Hockey−stick identity) |
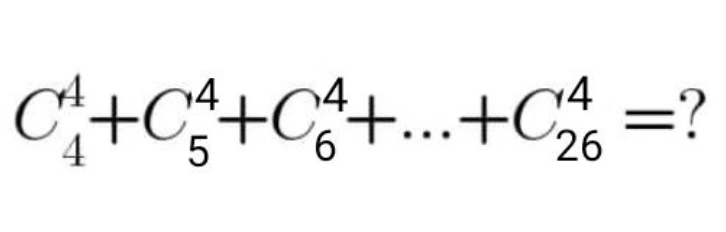
|
| C_4 ^4 +C_4 ^5 +C_4 ^6 +...+C_4 ^(26) =? |