
Question and Answers Forum
Question Number 88170 by Ar Brandon last updated on 08/Apr/20
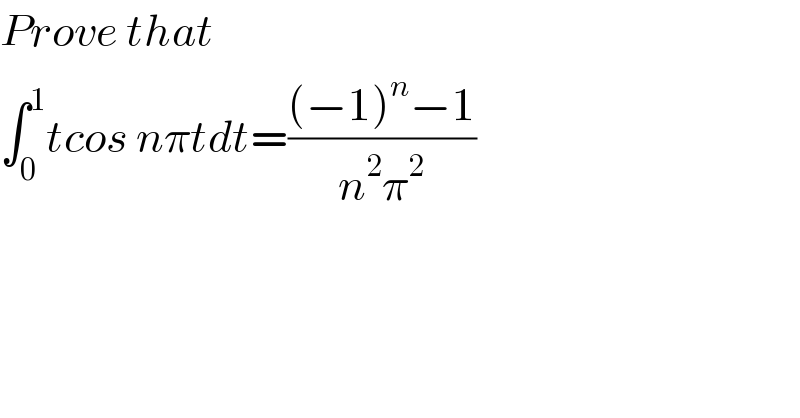
Commented by jagoll last updated on 08/Apr/20
![= ((t.sin nπt)/(nπ)) + ((cos nπt)/(n^2 π^2 )) ] _0^1 = ((sin nπ)/(nπ)) + ((cos nπ)/(n^2 π^2 )) − (1/(n^2 π^2 )) = (((−1)^n −1)/(n^2 π^2 ))](Q88172.png)
Commented by Joel578 last updated on 08/Apr/20

| ||
Question and Answers Forum | ||
Question Number 88170 by Ar Brandon last updated on 08/Apr/20 | ||
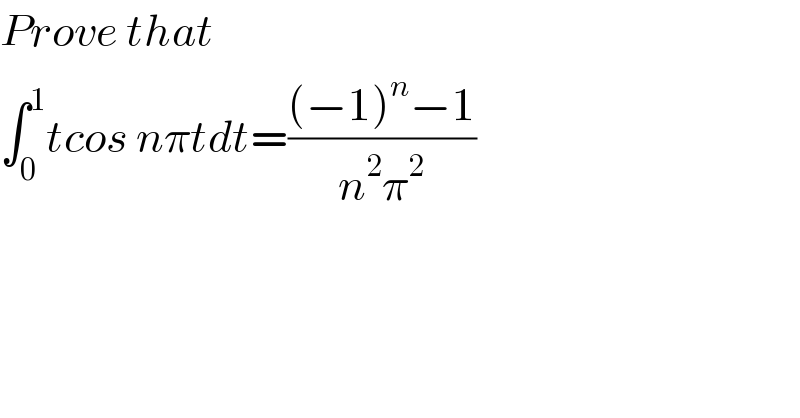 | ||
Commented by jagoll last updated on 08/Apr/20 | ||
![= ((t.sin nπt)/(nπ)) + ((cos nπt)/(n^2 π^2 )) ] _0^1 = ((sin nπ)/(nπ)) + ((cos nπ)/(n^2 π^2 )) − (1/(n^2 π^2 )) = (((−1)^n −1)/(n^2 π^2 ))](Q88172.png) | ||
Commented by Joel578 last updated on 08/Apr/20 | ||
 | ||