Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 51167 by Tawa1 last updated on 24/Dec/18
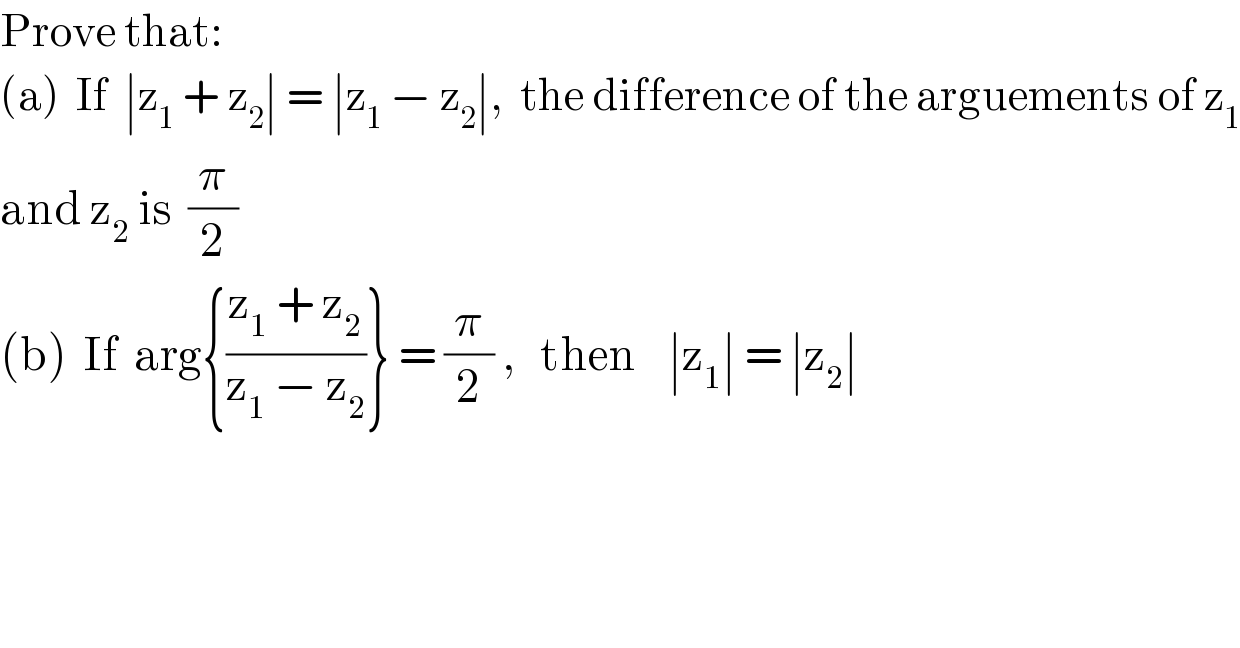
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Dec/18
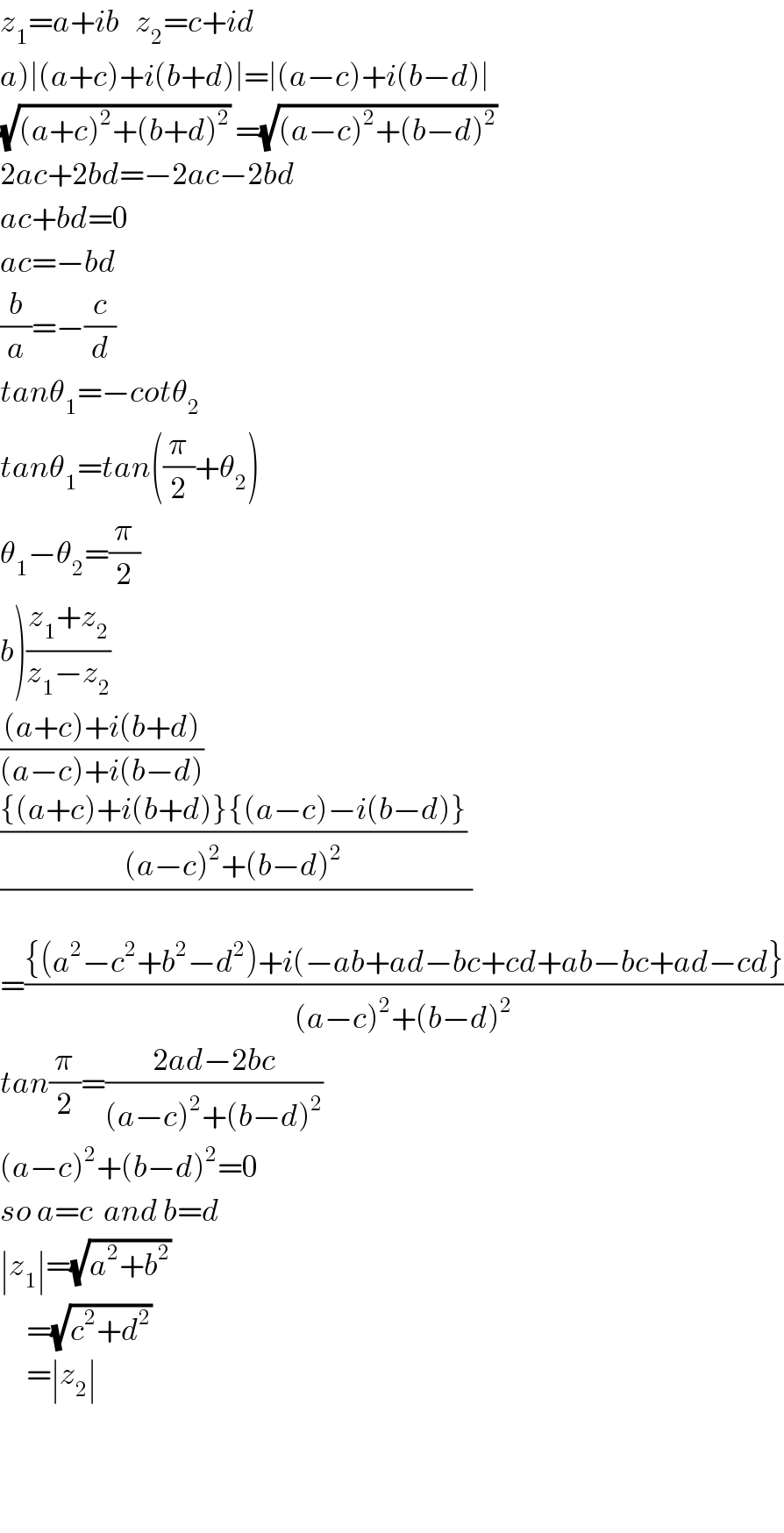
Commented by Tawa1 last updated on 24/Dec/18
Commented by Tawa1 last updated on 24/Dec/18
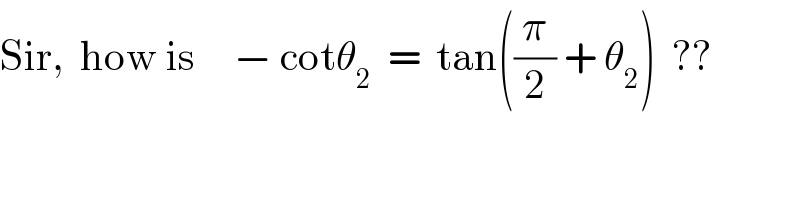
Commented by tanmay.chaudhury50@gmail.com last updated on 24/Dec/18
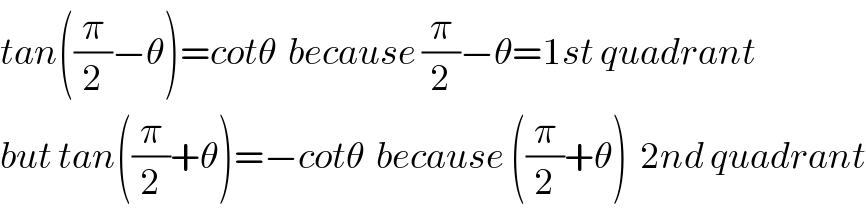
Commented by Tawa1 last updated on 24/Dec/18
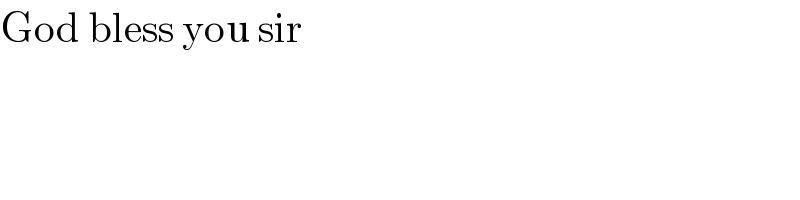
Answered by peter frank last updated on 24/Dec/18
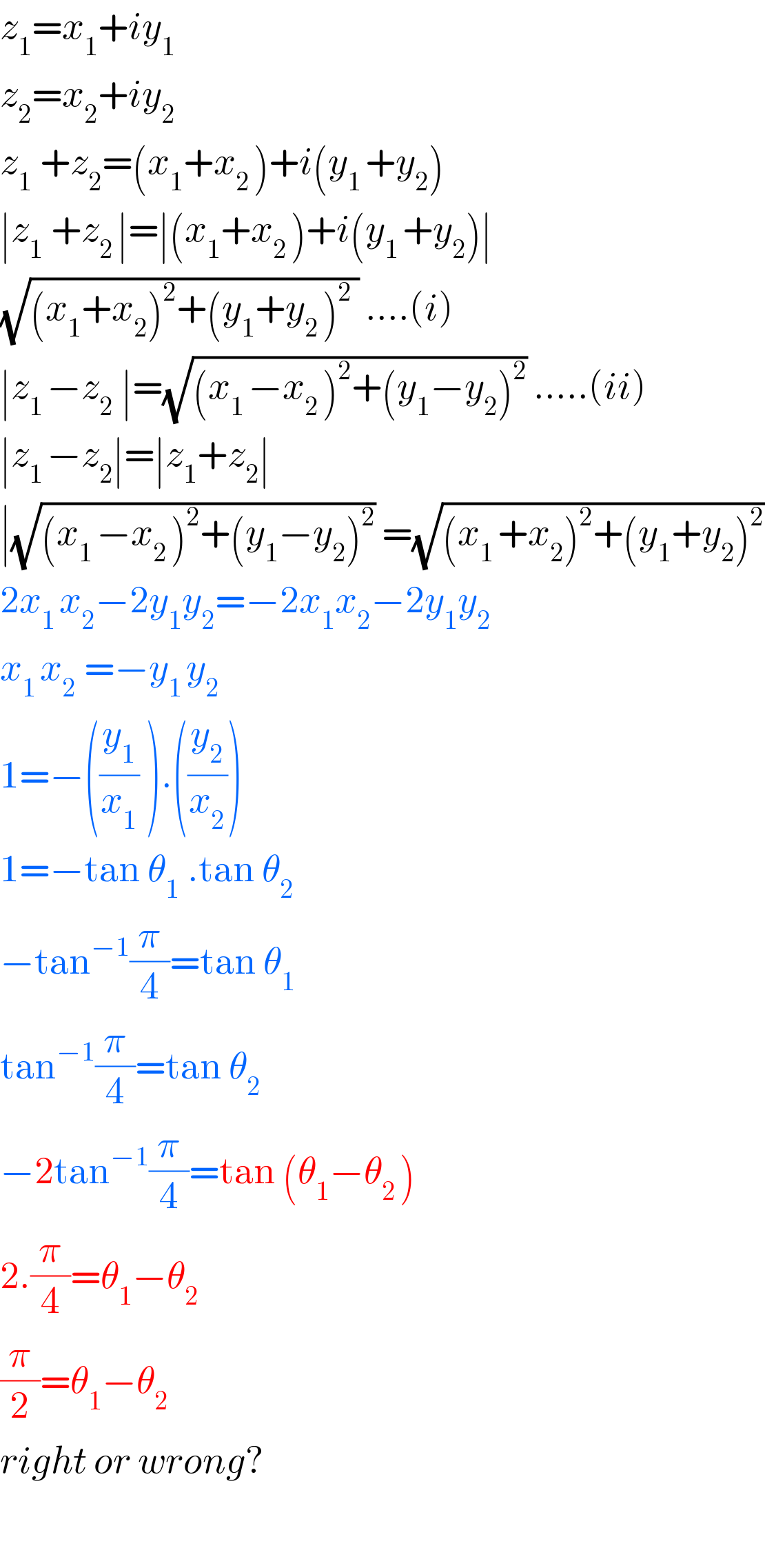
Commented by Tawa1 last updated on 24/Dec/18

Answered by peter frank last updated on 24/Dec/18
![[arg(z_1 +z_(2 ) )−arg(z_1 −z_2 )=(π/2) arg[(x_(1 ) +x_2 )+i(y_1 +y_2 )]−[arg(x_1 −x_2 +i(y_1 −y_2 )] tan^(−1) (((y_(1 ) +y_2 )/(x_1 +x_2 )))−tan^(−1) (((y_1 −y_2 )/(x_1 −x_2 )))=(π/2) (((y_(1 ) +y_2 )/(x_1 +x_2 )))+(((y_1 −y_2 )/(x_1 −x_2 )))÷[1−(((y_1 +y_2 )/(x_1 +x_2 ))).(((y_1 −y_2 )/(x_(1 ) −x_2 )))=(π/2) (((y_(1 ) +y_2 )/(x_1 +x_2 )))+(((y_1 −y_2 )/(x_1 −x_2 )))÷[1−(((y_1 +y_2 )/(x_1 +x_2 ))).(((y_1 −y_2 )/(x_(1 ) −x_2 )))=(1/0) x_1 ^2 −x_2 ^2 +y_2 ^2 −y_1 ^2 =0 x_1 ^2 +y_1 ^2 −x_2 ^2 −y_2 ^2 =0 x_1 ^2 +y_1 ^2 =x_2 ^2 +y_(2 ) ^2 ∣z_(1 ) ∣=∣z_2 ∣](Q51202.png)
Commented by Tawa1 last updated on 24/Dec/18