
Question and Answers Forum
Question Number 19900 by Tinkutara last updated on 17/Aug/17
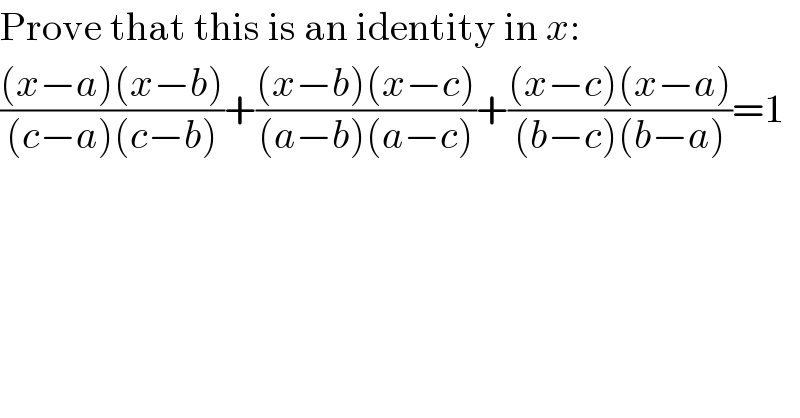
Answered by Rasheed.Sindhi last updated on 17/Aug/17
![−(((x−a)(x−b))/((c−a)(b−c)))−(((x−b)(x−c))/((a−b)(c−a)))−(((x−c)(x−a))/((b−c)(a−b)))=1 ((−(a−b)(x−a)(x−b)−(b−c)(x−b)(x−c)−(c−a)(x−c)(x−a))/((a−b)(b−c)(c−a)))=1 −(((a−b)(x^2 −(a+b)x+ab)+(b−c)(x^2 −(b+c)x+bc)+(c−a)(x^2 −(c+a)x+ca))/((a−b)(b−c)(c−a)))=1 −(([(a−b)+(b−c)+(c−a)]x^2 −[(a^2 −b^2 )+(b^2 −c^2 )+(c^2 −a^2 )]x+ab(a−b)+bc(b−c)+ca(c−a))/((a−b)(b−c)(c−a)))=1 −((0x^2 −0x+ab(a−b)+bc(b−c)+ca(c−a))/((a−b)(b−c)(c−a)))=1 −((ab(a−b)+bc(b−c)+ca(c−a))/((a−b)(b−c)(c−a)))=1 −((a^2 b−ab^2 +b^2 c−bc^2 +c^2 a−ca^2 )/((a−b)(b−c)(c−a)))=1 −((a^2 b−ab^2 +b^2 c−ca^2 −bc^2 +c^2 a)/((a−b)(b−c)(c−a)))=1 −((ab(a−b)−c(a^2 −b^2 )+c^2 (a−b))/((a−b)(b−c)(c−a)))=1 −(((a−b)[ab−c(a+b)+c^2 ])/((a−b)(b−c)(c−a)))=1 −(((a−b)[c^2 −ca−cb+ab])/((a−b)(b−c)(c−a)))=1 −(((a−b)[c(c−a)−b(c−a)])/((a−b)(b−c)(c−a)))=1 −(((a−b)[c(c−a)−b(c−a)])/((a−b)(b−c)(c−a)))=1 −(((a−b)(c−b)(c−a))/((a−b)(b−c)(c−a)))=1 (((a−b)(b−c)(c−a))/((a−b)(b−c)(c−a)))=1 1=1 Free of x. I.e the equation is true for all values of x. That means the given equation is an identity in x.](Q19902.png)
Commented by Tinkutara last updated on 17/Aug/17
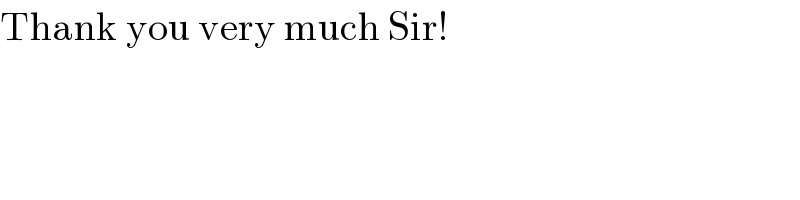
Answered by ajfour last updated on 17/Aug/17
![T_1 +T_2 =(((b−a)(x−a)(x−b)+(c−b)(x−b)(x−c))/((a−b)(b−c)(c−a))) =(((x−b)[x(c−a)−ab+a^2 +bc−c^2 ])/((a−b)(b−c)(c−a))) =(((x−b)[x(c−a)+b(c−a)−(c+a)(c−a)])/((a−b)(b−c)(c−a))) =(((x−b)(x+b−a−c))/((a−b)(b−c))) =(([x^2 −(a+c)x+ac]+[−b^2 +ab+bc−ac])/((a−b)(b−c))) =(((x−c)(x−a))/((a−b)(b−c)))+(((a−b)(b−c))/((a−b)(b−c))) T_1 +T_2 =−T_3 +1 or T_1 +T_2 +T_3 =1 (T_i being the i^(th) term on l.h.s. ) .](Q19908.png)
Commented by Tinkutara last updated on 17/Aug/17

