Question and Answers Forum
Question Number 19292 by Tinkutara last updated on 08/Aug/17
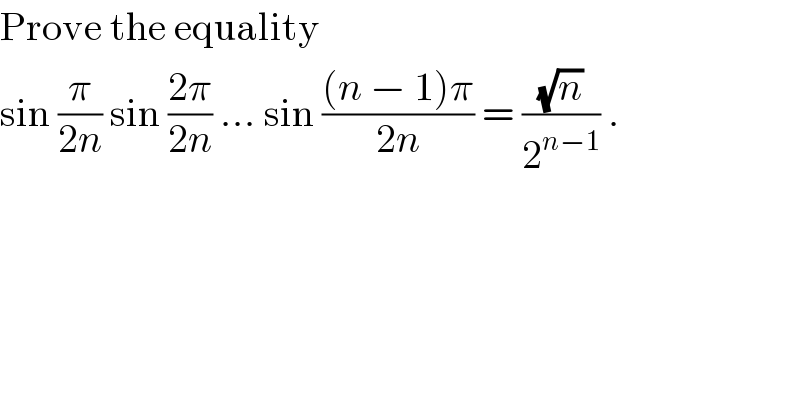
Commented by prakash jain last updated on 09/Aug/17
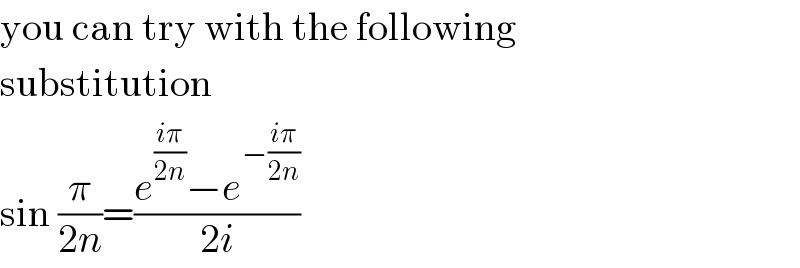
Answered by Tinkutara last updated on 23/Aug/17
![x^(2n) −1=(x−1)(x−α)(x−α^2 )....(x−α^(2n−1) ) where α = e^(((2π)/(2n))i) = e^((π/n)i) On differentiating both sides, 2nx^(2n−1) =(x−α)(x−α^2 )....(x−α^(2n−1) ) +(x−1)(x−α^2 )(x−α^3 )....(x−α^(2n−1) ) +(x−1)(x−α)(x−α^3 )....+.... Put x = 1 2n=(1−α)(1−α^2 )(1−α^3 )....(1−α^(2n−1) ) Since 1 − e^(iθ) = 2 sin (θ/2) e^(((θ/2) − (π/2))i) 2n=(1−e^((π/n)i) )(1−e^(((2π)/n)i) )(1−e^(((3π)/n)i) )....(1−e^((π/n)(2n−1)i) ) =2^(2n−1) sin(π/(2n))sin((2π)/(2n))....sin(((2n−1)π)/(2n))e^(((π/(2n))−(π/2))i) e^((((2π)/(2n))−(π/2))i) ....e^((((π(2n−1))/(2n))−(π/2))i) =2^(2n−1) sin(π/(2n))sin((2π)/(2n))....sin(((2n−1)π)/(2n))e^(i[(π/(2n))(((2n(2n−1))/2))−(2n−1)(π/2)]) 2n=2^(2n−1) sin(π/(2n))sin((2π)/(2n))....sin(((2n−1)π)/(2n))e^0 ((2n)/2^(2n−1) )=sin(π/(2n))sin((2π)/(2n))....sin(((n−1)π)/(2n))sin((nπ)/(2n))....sin(π/(2n)) (n/2^(2n−2) ) = sin^2 (π/(2n)) sin^2 ((2π)/(2n)) .... sin^2 (((n−1)π)/(2n)) ((√n)/2^(n−1) ) = sin (π/(2n)) sin ((2π)/(2n)) .... sin (((n−1)π)/(2n))](Q20189.png)
| ||
Question and Answers Forum | ||
| ||
Question Number 19292 by Tinkutara last updated on 08/Aug/17 | ||
| ||
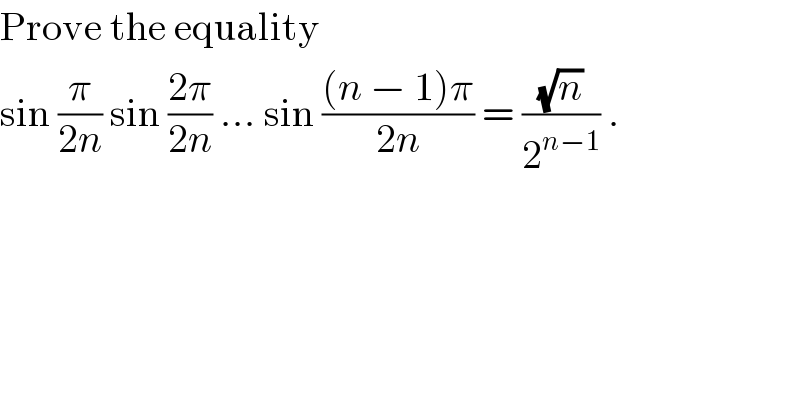Commented by prakash jain last updated on 09/Aug/17 | ||
| ||
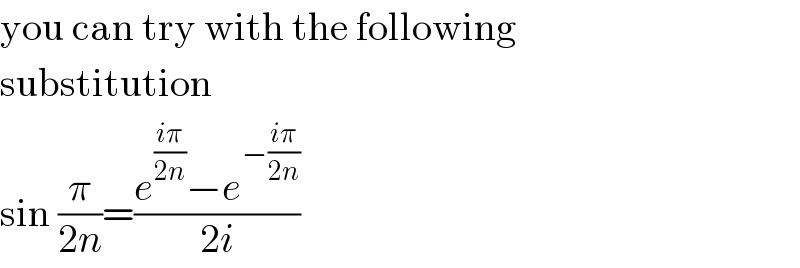Answered by Tinkutara last updated on 23/Aug/17 | ||
| ||
| ||