Question and Answers Forum
Question Number 103345 by harckinwunmy last updated on 14/Jul/20

Commented by harckinwunmy last updated on 14/Jul/20

Commented by Dwaipayan Shikari last updated on 14/Jul/20
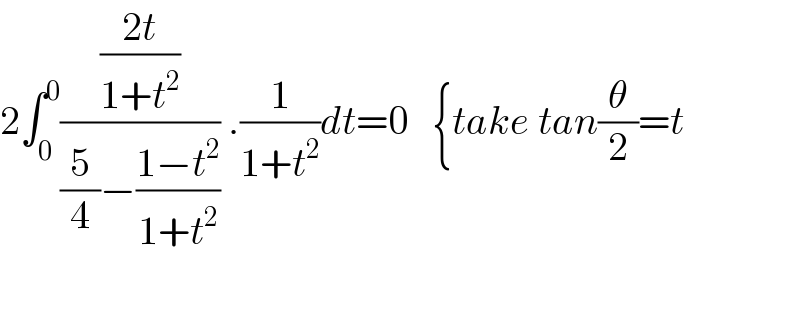
Commented by mathmax by abdo last updated on 14/Jul/20
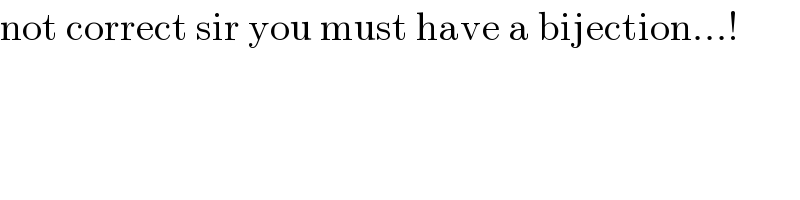
Commented by Dwaipayan Shikari last updated on 14/Jul/20

Commented by mathmax by abdo last updated on 15/Jul/20
![tan is bijective on ]−(π/2),(π/2)[ not [0,2π] be carefull](Q103433.png)
Answered by abdomathmax last updated on 14/Jul/20
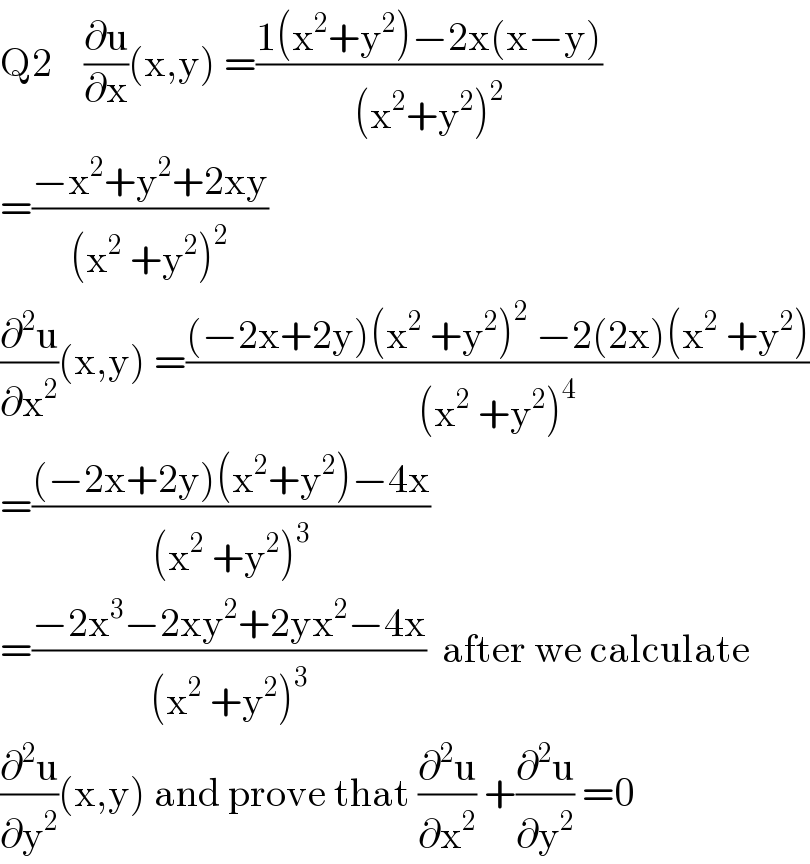
Answered by abdomathmax last updated on 14/Jul/20
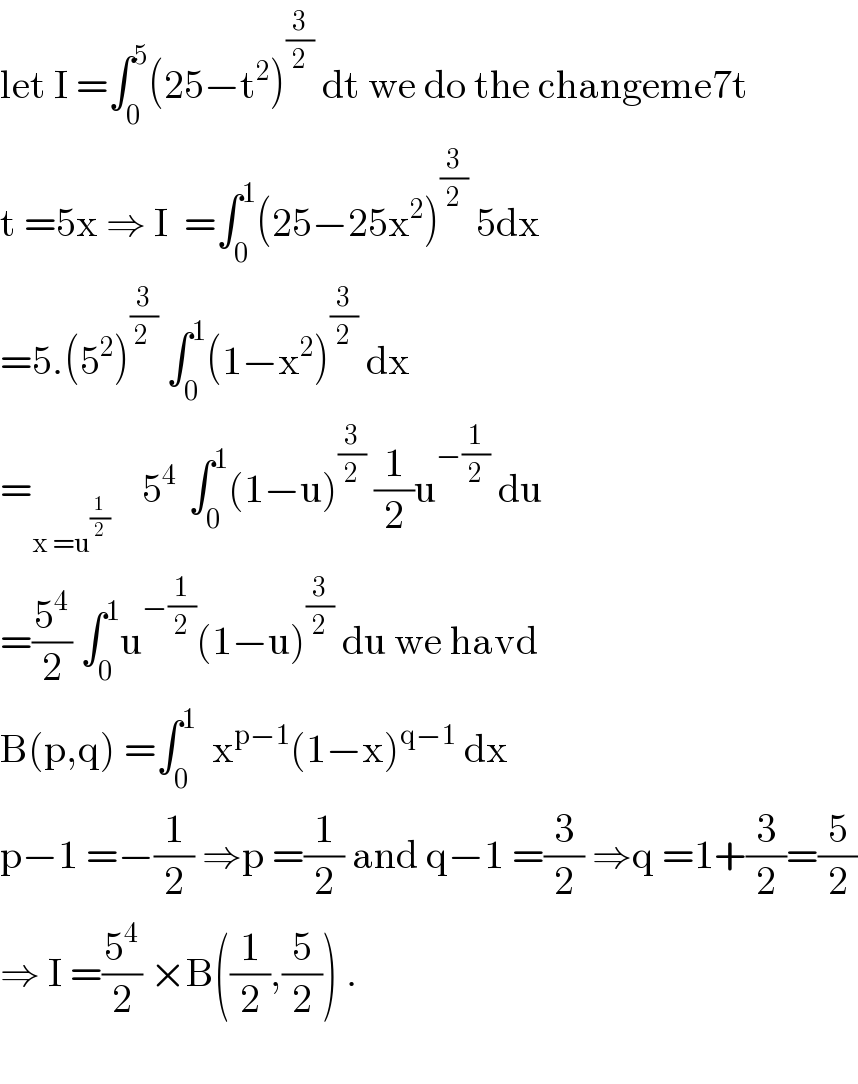
Answered by abdomathmax last updated on 14/Jul/20
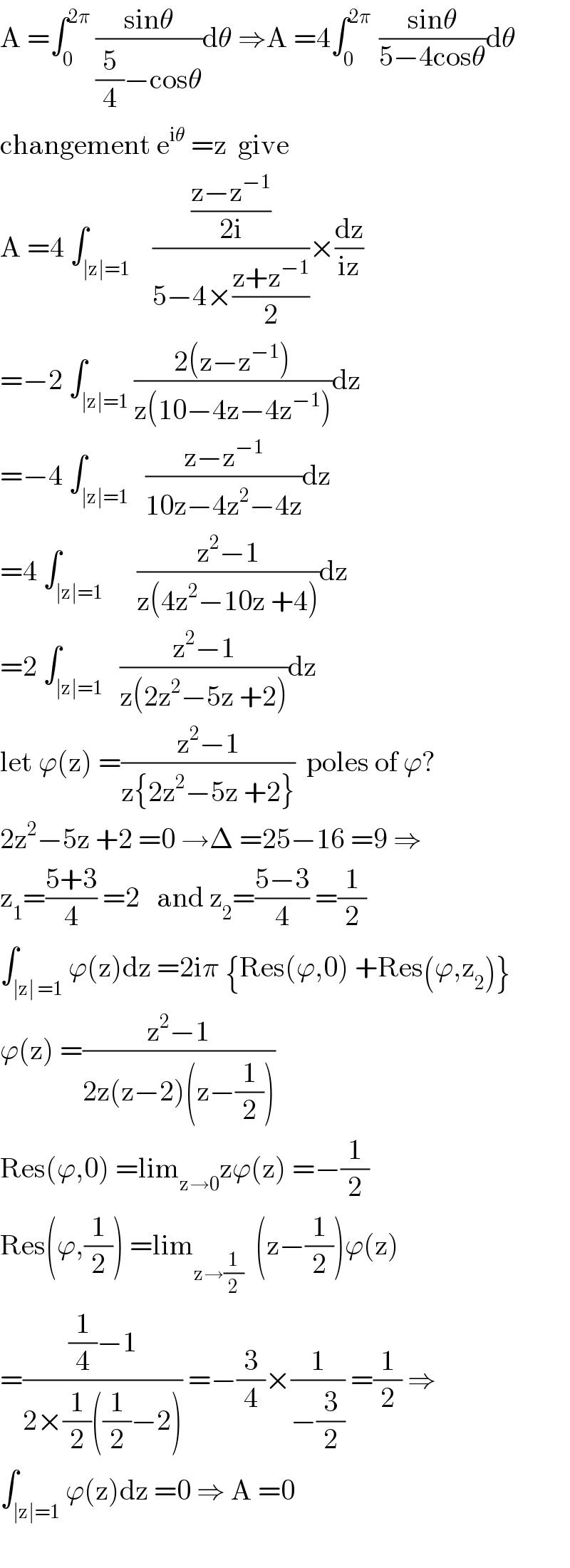
Answered by 1549442205 last updated on 15/Jul/20