Math Question and Answers


Question and Answers Forum

All Questions Topic List
Mechanics Questions
Previous in All Question Next in All Question
Previous in Mechanics Next in Mechanics
Question Number 109268 by mr W last updated on 22/Aug/20

Commented by mr W last updated on 22/Aug/20

$b l o c k m i s r e l e a s e d a t h e i g h t h .$ $f i n d t h e t i m e i t n e e d s t o r e a c h t h e$ $g r o u n d .$ $a l l m o t i o n i s f r i c t i o n l e s s .$
Commented by Dwaipayan Shikari last updated on 22/Aug/20

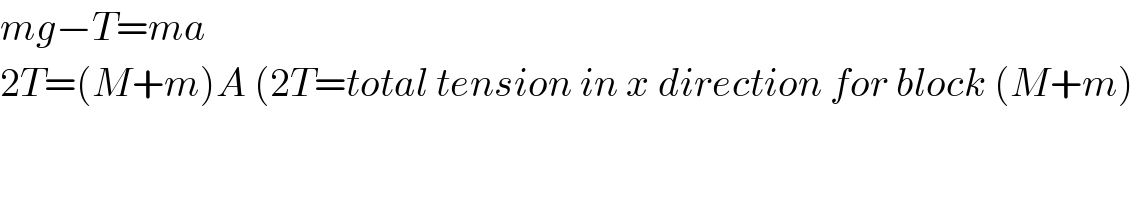
$m g - T = m a$ $2 T = (M + m) A (2 T = t o t a l t e n s i o n i n x d i r e c t i o n f o r b l o c k (M + m)$
Commented by mr W last updated on 22/Aug/20

$n o t c o r r e c t s i r!$ $y o u a s s u m e d t h a t m a n d M h a v e t h e$ $s a m e a c c e l e r a t i o n i n x d i r e c t i o n, b u t$ $t h i s i s o n l y t h e c a s e w h e n t h e s t r i n g$ $h o l d i n g m i s i n c l i n e d, b u t t h i s m e a n s$ $t h a t t h e a c c e l e r a t i o n o f m i n y$ $d i r e c t i o n i s n o t e q u a l t o a a s y o u$ $a s s u m e d .$ $b e s i d e s y o u w r o t e 2 T = (M + m) a,$ $h o w d i d y o u g e t 2 T ?$
Commented by mr W last updated on 22/Aug/20

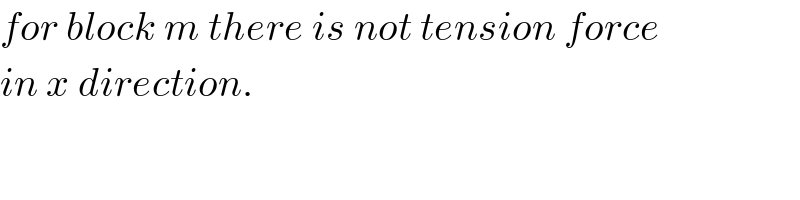
$f o r b l o c k m t h e r e i s n o t t e n s i o n f o r c e$ $i n x d i r e c t i o n .$
Commented by Dwaipayan Shikari last updated on 22/Aug/20

$I h a v e a s s u m e d (M + m) a s s y s t e m . i f M g o e s i n x d i r e c t i o n t h e n$ $m a s s w i l l a l s o m o v e i n x d i r e c t i o n$
	Answered by mr W last updated on 22/Aug/20

	Commented by ajfour last updated on 22/Aug/20

	$T (1 - \sin θ) = M (\frac{d^{2} s}{{d t}^{2}})$ $m g \cos θ + m (\frac{d^{2} s}{{d t}^{2}}) \sin θ - T = m [\frac{d^{2} s}{{d t}^{2}} - R {(\frac{d θ}{d t})}^{2}]$ $m (\frac{d^{2} s}{{d t}^{2}}) \cos θ - m g \sin θ = m s (\frac{d^{2} θ}{{d t}^{2}})$ $- - - - - - - - - - - - - - - - - -$ $l e t \frac{M}{m} = k \Rightarrow$ $g \cos θ + (\frac{d^{2} s}{{d t}^{2}}) \sin θ - \frac{k}{(1 - \sin θ)} (\frac{d^{2} s}{{d t}^{2}})$ $= \frac{d^{2} s}{{d t}^{2}} - R {(\frac{d θ}{d t})}^{2} &$ $\frac{d^{2} s}{{d t}^{2}} \cos θ - g \sin θ = s (\frac{d^{2} θ}{{d t}^{2}})$ $. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .$
	Commented by mr W last updated on 22/Aug/20

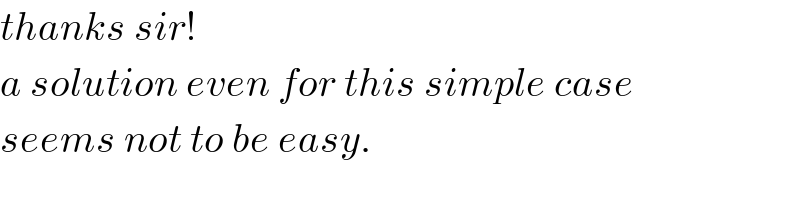
	$t h a n k s s i r!$ $a s o l u t i o n e v e n f o r t h i s s i m p l e c a s e$ $s e e m s n o t t o b e e a s y .$
	Commented by ajfour last updated on 22/Aug/20
	$mg−Tcos θ=m((d^2 y/dt^2 )) T(1−sin θ)=M((d^2 s/dt^2 )) m((d^2 s/dt^2 ))−Tsin θ=m((d^2 X/dt^2 )) tan θ=(X/y) −−−−−−−−−−−−−−−− g−(T/m)((y/s))=(d^2 y/dt^2 ) .....(i) (T/m)(1−(X/s))=k((d^2 s/dt^2 )) ......(ii) (d^2 s/dt^2 )−(T/m)((X/s))=(d^2 X/dt^2 ) ......(iii) −−−−−−−−−−−−−−−− from (ii) & (iii) (d^2 s/dt^2 ){1−(k/(((s/X)−1)))}=(d^2 X/dt^2 ) let (s/X) = z ⇒ d^2 (Xz){1−(k/(z−1))}=d^2 X (1−(k/(z−1)))d(zdX+Xdz)=d(dX) .......$
	$m g - T \cos θ = m (\frac{d^{2} y}{{d t}^{2}})$ $T (1 - \sin θ) = M (\frac{d^{2} s}{{d t}^{2}})$ $m (\frac{d^{2} s}{{d t}^{2}}) - T \sin θ = m (\frac{d^{2} X}{{d t}^{2}})$ $\tan θ = \frac{X}{y}$ $- - - - - - - - - - - - - - - -$ $g - \frac{T}{m} (\frac{y}{s}) = \frac{d^{2} y}{{d t}^{2}} . . . . . (i)$ $\frac{T}{m} (1 - \frac{X}{s}) = k (\frac{d^{2} s}{{d t}^{2}}) . . . . . . (i i)$ $\frac{d^{2} s}{{d t}^{2}} - \frac{T}{m} (\frac{X}{s}) = \frac{d^{2} X}{{d t}^{2}} . . . . . . (i i i)$ $- - - - - - - - - - - - - - - -$ $f r o m (i i) & (i i i)$ $\frac{d^{2} s}{{d t}^{2}} {1 - \frac{k}{(\frac{s}{X} - 1)}} = \frac{d^{2} X}{{d t}^{2}}$ $l e t \frac{s}{X} = z$ $\Rightarrow d^{2} (X z) {1 - \frac{k}{z - 1}} = d^{2} X$ $(1 - \frac{k}{z - 1}) d (z d X + X d z) = d (d X)$ $. . . . . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum