Math Question and Answers


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 119979 by huotpat last updated on 28/Oct/20

Commented by huotpat last updated on 28/Oct/20

$N w h e n n \to + \infty i s n o t x \to + \infty$
	Answered by mathmax by abdo last updated on 28/Oct/20

	$let f (x) = \frac{{(x + 1)}^{n + 1} - (x + 1)}{x^{3}} - \frac{n}{x^{2}} - \frac{n (n + 1)}{2 x} \Rightarrow$ $f (x) = \frac{{(x + 1)}^{n + 1} - (x + 1) - nx - 2^{- 1} n (n + 1) x^{2}}{x^{3}} we knowthat$ ${(1 + x)}^{α} = 1 + \frac{α}{1!} x + \frac{α (α - 1)}{2!} x^{2} + \frac{α (α - 1) (α - 2)}{3!} x^{3} + o (x^{4}) \Rightarrow$ ${(1 + x)}^{n + 1} = 1 + (n + 1) x + \frac{(n + 1) n}{2} x^{2} + \frac{(n + 1) n (n - 1)}{6} x^{3} + o (x^{4}) \Rightarrow$ ${(x + 1)}^{n + 1} - (x + 1) - nx - 2^{- 1} n (n + 1) x^{2} \sim$ $1 + (n + 1) x + \frac{n (n + 1)}{2} x^{2} + \frac{(n - 1) n (n + 1)}{6} x^{3} - x - 1 - nx - \frac{1}{2} n (n + 1) x^{2}$ $= \frac{n (n - 1) (n + 1)}{6} x^{3} \Rightarrow f (x) \sim \frac{n (n - 1) (n + 1)}{6} \Rightarrow$ $\lim_{x \to 0} f (x) = \frac{n (n - 1) (n + 1)}{6}$
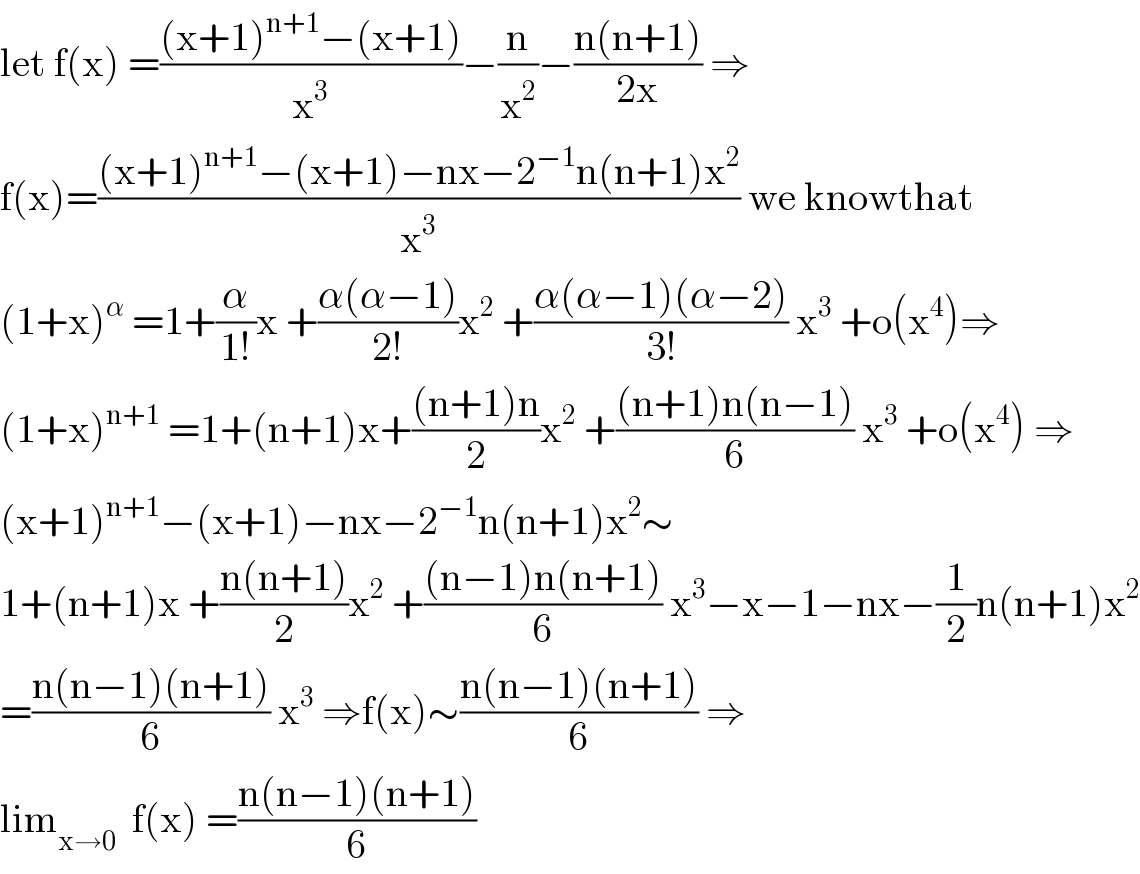
	Answered by Dwaipayan Shikari last updated on 28/Oct/20

	$\lim_{n \to + \infty} n [\underset{p}{\prod^{n}} (\underset{k = 1}{\sum^{p}} \frac{1}{k} - \frac{1}{k + 1})]$ $\lim_{n \to + \infty} n [\underset{p}{\prod^{n}} (1 - \frac{1}{p + 1})]$ $\lim_{n \to + \infty} n [\underset{p}{\prod^{n}} \frac{p}{p + 1}] = n . \frac{1}{2} . \frac{2}{3} . \frac{3}{4} . . . . . . \frac{1}{n} . \frac{n}{n + 1}$ $\lim_{n \to \infty} = \frac{n}{1 + n} = \frac{1}{1 + \frac{1}{n}} = 1$
	Answered by mathmax by abdo last updated on 28/Oct/20
	$let g(x) =((x+2x^2 +3x^3 +...+nx^n )/(x−1))−((n(n+1))/(2(x−1))) (x→1) we have 1+x +x^2 +...+x^n =((x^(n+1) −1)/(x−1)) (x≠1) by d erivation we get 1+2x+...+nx^(n−1) =(dx/dx)(((x^(n+1) −1)/(x−1))) =((nx^(n+1) −(n+1)x^n +1)/((x−1)^2 )) ⇒ x +2x^2 +3x^3 +....+nx^n =((nx^(n+2) −(n+1)x^(n+1) +x)/((x−1)^2 )) ⇒ g(x)=((nx^(n+2) −(n+1)x^(n+1) +x)/((x−1)^2 ))−((n(n+1))/(2(x−1))) ⇒ g(x)=((2nx^(n+2) −2(n+1)x^(n+1) +2x)/(2(x−1)^2 ))−((n(n+1)(x−1))/(2(x−1)^2 )) =((2nx^(n+2) −2(n+1)x^(n+1) +2x−n(n+1)(x−1))/(2(x−1)^2 )) let u(x)=2nx^(n+2) −2(n+1)x^(n+1) +2x−n(n+1)(x−1) v(x)=2(x−1)^2 ⇒ u^′ (x)=2n(n+2)x^(n+1) −2(n+1)^2 x^n +2−n(n+1) u^((2)) (x) =2n(n+2)(n+1)x^n −2n(n+1)^2 x^(n−1) ⇒ u^((2)) (1) =2n(n+2)(n+1)−2n(n+1)^2 =2n(n+1){n+2−n−1) =2n(n+1) v(x)=2(x−1)^2 ⇒v^′ (x)=4(x−1) ⇒v^((2)) (x)=4 ⇒ lim_(x→1) g(x) =lim_(x→1) ((u^((2)) (x))/(v^((2)) (x))) =((2n(n+1))/4) =((n(n+1))/2)$
	$let g (x) = \frac{x + {2 x}^{2} + {3 x}^{3} + . . . + {nx}^{n}}{x - 1} - \frac{n (n + 1)}{2 (x - 1)} (x \to 1)$ $we have 1 + x + x^{2} + . . . + x^{n} = \frac{x^{n + 1} - 1}{x - 1} (x \neq 1) by d erivation we get$ $1 + 2 x + . . . + {nx}^{n - 1} = \frac{dx}{dx} (\frac{x^{n + 1} - 1}{x - 1}) = \frac{{nx}^{n + 1} - (n + 1) x^{n} + 1}{{(x - 1)}^{2}} \Rightarrow$ $x + {2 x}^{2} + {3 x}^{3} + . . . . + {nx}^{n} = \frac{{nx}^{n + 2} - (n + 1) x^{n + 1} + x}{{(x - 1)}^{2}} \Rightarrow$ $g (x) = \frac{{nx}^{n + 2} - (n + 1) x^{n + 1} + x}{{(x - 1)}^{2}} - \frac{n (n + 1)}{2 (x - 1)} \Rightarrow$ $g (x) = \frac{{2 nx}^{n + 2} - 2 (n + 1) x^{n + 1} + 2 x}{2 {(x - 1)}^{2}} - \frac{n (n + 1) (x - 1)}{2 {(x - 1)}^{2}}$ $= \frac{{2 nx}^{n + 2} - 2 (n + 1) x^{n + 1} + 2 x - n (n + 1) (x - 1)}{2 {(x - 1)}^{2}}$ $let u (x) = {2 nx}^{n + 2} - 2 (n + 1) x^{n + 1} + 2 x - n (n + 1) (x - 1)$ $v (x) = 2 {(x - 1)}^{2} \Rightarrow$ $u^{^{'}} (x) = 2 n (n + 2) x^{n + 1} - 2 {(n + 1)}^{2} x^{n} + 2 - n (n + 1)$ $u^{(2)} (x) = 2 n (n + 2) (n + 1) x^{n} - 2 n {(n + 1)}^{2} x^{n - 1} \Rightarrow$ $u^{(2)} (1) = 2 n (n + 2) (n + 1) - 2 n {(n + 1)}^{2}$ $= 2 n (n + 1) {n + 2 - n - 1) = 2 n (n + 1)$ $v (x) = 2 {(x - 1)}^{2} \Rightarrow v^{^{'}} (x) = 4 (x - 1) \Rightarrow v^{(2)} (x) = 4 \Rightarrow$ $\lim_{x \to 1} g (x) = \lim_{x \to 1} \frac{u^{(2)} (x)}{v^{(2)} (x)} = \frac{2 n (n + 1)}{4} = \frac{n (n + 1)}{2}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum