
Question and Answers Forum
Question Number 12846 by Joel577 last updated on 04/May/17

Commented by Joel577 last updated on 04/May/17

Answered by mrW1 last updated on 04/May/17
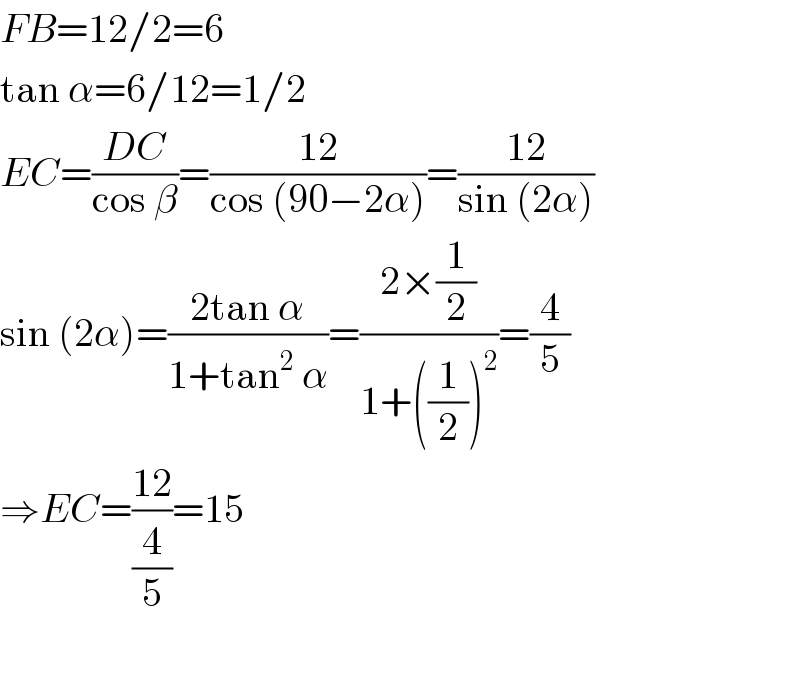
Commented by mrW1 last updated on 04/May/17
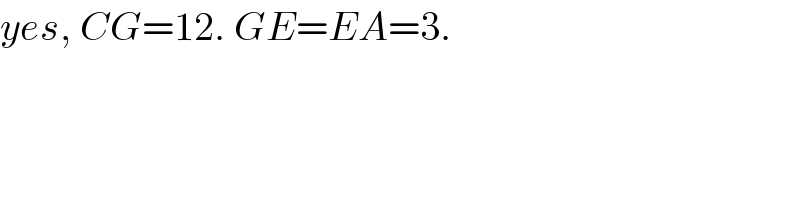
Commented by mrW1 last updated on 04/May/17

Commented by Joel577 last updated on 04/May/17
Commented by Joel577 last updated on 04/May/17

Commented by mrW1 last updated on 04/May/17
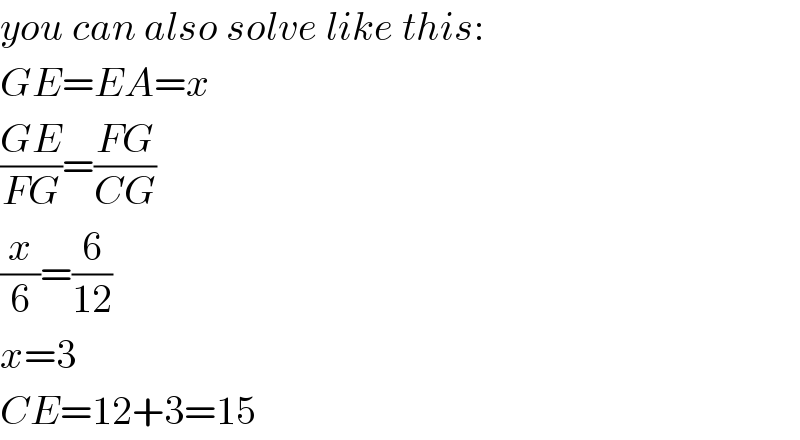
Commented by chux last updated on 04/May/17

Commented by Joel577 last updated on 04/May/17

Commented by A Haq Soomro last updated on 06/May/17

Answered by ajfour last updated on 04/May/17

Commented by ajfour last updated on 04/May/17
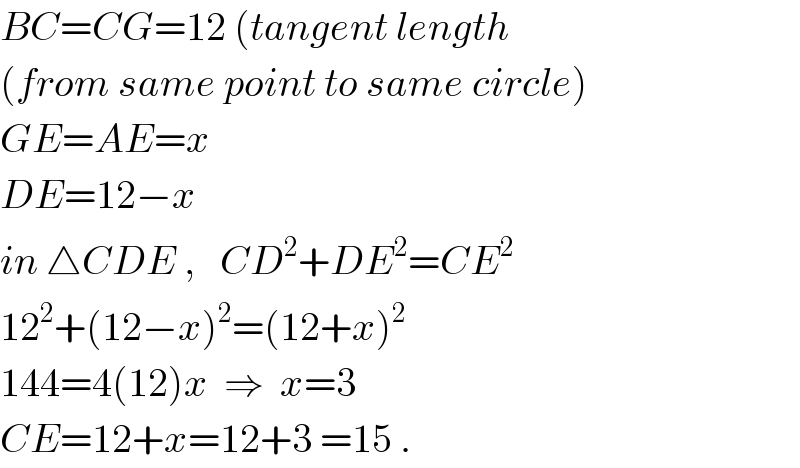
Commented by chux last updated on 04/May/17
Commented by A Haq Soomro last updated on 06/May/17

