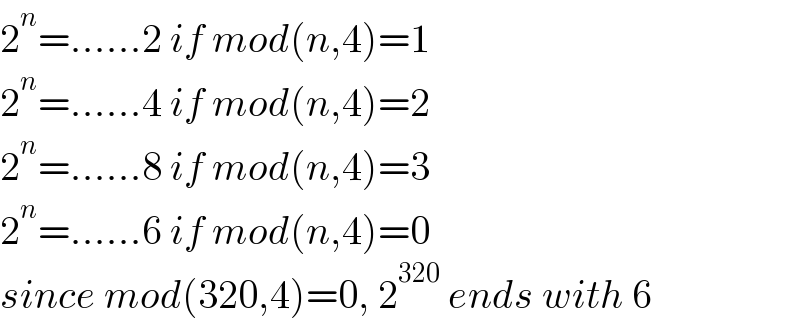Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 130727 by EDWIN88 last updated on 28/Jan/21

Commented by MJS_new last updated on 28/Jan/21

$$6$$

Commented by EDWIN88 last updated on 28/Jan/21

$$yes$$

Answered by liberty last updated on 28/Jan/21

$$2^{5\mathrm{k}}=2\left(\mathrm{mod}10\right)\mathrm{\forall }\mathrm{k}\in {\mathbb{Z}}^{+}$$$$320=25\times 12+5\times 4$$$$2^{320}={\left[{\left(2^5\right)}^5\right]}^{12}\times {\left(2^5\right)}^4\left(\mathrm{mod}10\right)$$$$={\left[{\left(2\right)}^5\right]}^2\times \left(2^4\right)\times 2^2\left(\mathrm{mod}10\right)$$$$=2^2\times 2^6=2^5\times 2^3=16\left(\mathrm{mod}10\right)$$$$=6\left(\mathrm{mod}10\right)$$

Commented by JDamian last updated on 29/Jan/21

$$2^{5k}\ne 2\left(mod10\right)$$$$k=2\Rightarrow 2^{10}=1024$$

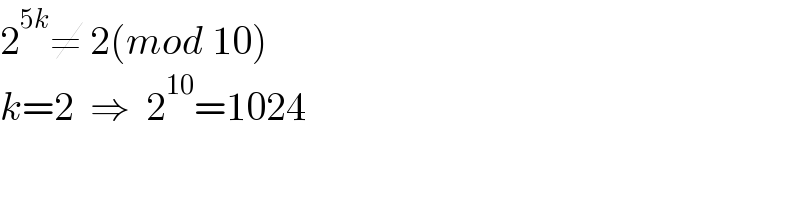
Answered by mr W last updated on 28/Jan/21

$$2^n=......2ifmod(n,4)=1$$$$2^n=......4ifmod(n,4)=2$$$$2^n=......8ifmod(n,4)=3$$$$2^n=......6ifmod(n,4)=0$$$$sincemod(320,4)=0,2^{320}endswith6$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com