Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 13977 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 25/May/17

Commented by prakash jain last updated on 26/May/17
$∫((3+x^2 )/(2+x^3 ))dx ∫(3/((2^(1/3) )^3 +x^3 ))dx+∫(x^2 /(2+x^3 ))dx ∫(x^2 /(2+x^3 ))dx=∫(du/(3(2+u))) (x^3 =u) =(1/3)ln (2+u)+C=(1/3)ln (2+x^3 ) −−−−−− (x^3 +2)=(x+2^(1/3) )(x+2^(1/3) w)(x+2^(1/3) w^2 ) (1,w,w^2 ) are cube roots of unity. for easier typing i will put 2^(1/3) =j ∫((3dx)/((x+j)(x+jw)(x+jw^2 ))) =∫(A/(x+j))dx+∫(B/(x+jw))dx+∫(C/(x+jw^2 ))dx perform partial fraction and integrate.$
$\int \frac{3 + x^{2}}{2 + x^{3}} d x$ $\int \frac{3}{{(2^{1 / 3})}^{3} + x^{3}} d x + \int \frac{x^{2}}{2 + x^{3}} d x$ $\int \frac{x^{2}}{2 + x^{3}} d x = \int \frac{d u}{3 (2 + u)} (x^{3} = u)$ $= \frac{1}{3} \ln (2 + u) + C = \frac{1}{3} \ln (2 + x^{3})$ $- - - - - -$ $(x^{3} + 2) = (x + 2^{1 / 3}) (x + 2^{1 / 3} w) (x + 2^{1 / 3} w^{2})$ $(1, w, w^{2}) are cube roots of unity .$ $f o r e a s i e r t y p i n g i w i l l p u t 2^{1 / 3} = j$ $\int \frac{3 d x}{(x + j) (x + j w) (x + {j w}^{2})}$ $= \int \frac{A}{x + j} d x + \int \frac{B}{x + j w} d x + \int \frac{C}{x + {j w}^{2}} d x$ $p e r f o r m p a r t i a l f r a c t i o n a n d$ $i n t e g r a t e .$
	Answered by ajfour last updated on 26/May/17

	$I = \int_{0}^{1} (\frac{x^{2} + 3}{x^{3} + 2}) d x$ $l e t a^{3} = 2$ $x^{3} + 2 = (x + a) (x^{2} - a x + a^{2})$ $f o r x = 1, (1 + a) (1 - a + a^{2}) = 3$ $\frac{x^{2} + 3}{x^{3} + 2} = \frac{A}{x + a} + \frac{B x + C}{x^{2} - a x + a^{2}}$ $A = \frac{1}{3} + \frac{a}{2}, B = \frac{2}{3} - \frac{a}{2}, C = \frac{2}{a} - \frac{a}{3}$ $I = A \ln (1 + \frac{1}{a}) + \frac{B}{2} \int_{0}^{1} \frac{(2 x - a) d x}{x^{2} - a x + a^{2}}$ $+ (C + \frac{a B}{2}) \int_{0}^{1} \frac{d x}{{(x - \frac{a}{2})}^{2} + {(\frac{a \sqrt{3}}{2})}^{2}}$ $I = A \ln (1 + \frac{1}{a}) + \frac{B}{2} \ln (\frac{1 - a + a^{2}}{a^{2}})$ $+ (C + \frac{a B}{2}) \frac{2}{a \sqrt{3}} [\tan^{- 1} (\frac{a^{2} - 1}{\sqrt{3}}) + \frac{π}{6}]$ $s u b s t i t i n g f o r A, B, C a n d$ $u t i l i z i n g t h e f a c t a^{2} = \frac{2}{a},$ $t h a t a^{2} - a + 1 = \frac{3}{a + 1} w e h a v e$ $I = \frac{3 a}{4} \ln (1 + a) - (\frac{a}{4} + \frac{2}{3}) \ln a +$ $(\frac{1}{3} - \frac{a}{4}) \ln 3 + \frac{a \sqrt{3}}{2} [\tan^{- 1} (\frac{a^{2} - 1}{\sqrt{3}}) + \frac{π}{6}]$ $I = \frac{3 a}{4} \ln (1 + \frac{1}{a}) + \frac{a \sqrt{3}}{2} \tan^{- 1} (\frac{\sqrt{3}}{2 a - 1})$ $- \frac{a}{4} \ln (3 a) + \frac{2}{3} \ln (\frac{\sqrt{3}}{a}) .$
	Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 26/May/17

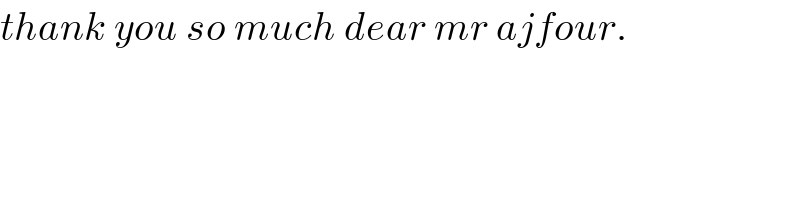
	$t h a n k y o u s o m u c h d e a r m r a j f o u r .$
	Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 26/May/17
	$A=(1/(2)^(1/3) )⇒t=Ax (x/(2)^(1/3) )=t⇒(x/(√3))=((t(2)^(1/3) )/(√3))=mt,m=((2)^(1/3) /(√3)),dx=(2)^(1/3) dt=m(√3)dt I=∫((3(1+((x/(√3)))^2 ))/(2(1+((x/(2)^(1/3) ))^3 )))dx=((3m(√3))/2)∫((1+mt^2 )/(1+t^3 ))dt =((3m(√3))/2)[∫(dt/(1+t^3 ))+m∫((t^2 dt)/(1+t^3 ))]=A[I_1 +mI_2 ] 1)I_2 =∫((t^2 dt)/(1+t^3 ))=(1/3)ln(1+t^3 )+C_2 2)I_1 =∫(dt/(1+t^3 ))=? (1/(1+t^3 ))=(a/(1+t))+((bx+c)/(1−t+t^2 )) { ((t=0⇒1=a+c)),((t=1⇒(1/2)=(a/2)+b+c)) :} t=−1⇒(1/3)=a+0⇒(a=(1/3),c=(2/3),b=((−1)/3)) ⇒(1/(1+t^3 ))=(1/(3(1+t)))+((−t+2)/(3(1−t+t^2 ))) ⇒I_1 =(1/3)∫((1/(1+t))+((−t+2)/(t^2 −t+1)))dt= =(1/3)∫((1/(1+t)))dt−(1/6)∫(((2t−1)−3)/(t^2 −t+1))dt= =(1/3)∫(dt/(1+t))−(1/6)∫(( 2t−1)/(t^2 −t+1))dt+((√3)/4)∫(dt/((((2t−1)/(√3)))^2 +1))= =(1/3)ln(1+t)−(1/6)ln(1−t+t^2 )+((√3)/4)tg^(−1) (((2t−1)/(√3)))+C_1 I=((3(2)^(1/3) )/2)[(1/3)ln(1+t)−(1/6)ln(1−t+t^2 )+↓ +((√3)/4)tg^(−1) (((2t−1)/(√3)))+((2)^(1/3) /(√3)).(1/3)ln(1+t^3 )]+C =(1/(8A))[4ln(1+Ax)−2ln(1−Ax+A^2 x^2 )+ +3(√3)tg^(−1) (((2Ax−1)/(√3)))+((4(√3))/(3A))ln(1+A^3 x^3 )]+C. F(1)=((2)^(1/3) /8)[4ln(1+(1/(2)^(1/3) ))−2ln(1−(1/(2)^(1/3) )+(1/(4)^(1/3) ))+ +3(√3)tg^(−1) ((((4)^(1/3) −1)/(√3)))+((4(2)^(1/3) )/(√3))ln(3/2)] F(0)=3(√3)tg^(−1) (−(1/(√3)))=−((π(√3))/2) . I=F(1)−F(0)=F(1)+((π(√3))/2) .$
	$A = \frac{1}{\sqrt[3]{2}} \Rightarrow t = A x$ $\frac{x}{\sqrt[3]{2}} = t \Rightarrow \frac{x}{\sqrt{3}} = \frac{t \sqrt[3]{2}}{\sqrt{3}} = m t, m = \frac{\sqrt[3]{2}}{\sqrt{3}}, d x = \sqrt[3]{2} d t = m \sqrt{3} d t$ $I = \int \frac{3 (1 + {(\frac{x}{\sqrt{3}})}^{2})}{2 (1 + {(\frac{x}{\sqrt[3]{2}})}^{3})} d x = \frac{3 m \sqrt{3}}{2} \int \frac{1 + {m t}^{2}}{1 + t^{3}} d t$ $= \frac{3 m \sqrt{3}}{2} [\int \frac{d t}{1 + t^{3}} + m \int \frac{t^{2} d t}{1 + t^{3}}] = A [I_{1} + {m I}_{2}]$ $1) I_{2} = \int \frac{t^{2} d t}{1 + t^{3}} = \frac{1}{3} l n (1 + t^{3}) + C_{2}$ $2) I_{1} = \int \frac{d t}{1 + t^{3}} = ?$ $\frac{1}{1 + t^{3}} = \frac{a}{1 + t} + \frac{b x + c}{1 - t + t^{2}} {\begin{cases} t = 0 \Rightarrow 1 = a + c \\ t = 1 \Rightarrow \frac{1}{2} = \frac{a}{2} + b + c \end{cases}$ $t = - 1 \Rightarrow \frac{1}{3} = a + 0 \Rightarrow (a = \frac{1}{3}, c = \frac{2}{3}, b = \frac{- 1}{3})$ $\Rightarrow \frac{1}{1 + t^{3}} = \frac{1}{3 (1 + t)} + \frac{- t + 2}{3 (1 - t + t^{2})}$ $\Rightarrow I_{1} = \frac{1}{3} \int (\frac{1}{1 + t} + \frac{- t + 2}{t^{2} - t + 1}) d t =$ $= \frac{1}{3} \int (\frac{1}{1 + t}) d t - \frac{1}{6} \int \frac{(2 t - 1) - 3}{t^{2} - t + 1} d t =$ $= \frac{1}{3} \int \frac{d t}{1 + t} - \frac{1}{6} \int \frac{2 t - 1}{t^{2} - t + 1} d t + \frac{\sqrt{3}}{4} \int \frac{d t}{{(\frac{2 t - 1}{\sqrt{3}})}^{2} + 1} =$ $= \frac{1}{3} l n (1 + t) - \frac{1}{6} l n (1 - t + t^{2}) + \frac{\sqrt{3}}{4} {t g}^{- 1} (\frac{2 t - 1}{\sqrt{3}}) + C_{1}$ $I = \frac{3 \sqrt[3]{2}}{2} [\frac{1}{3} l n (1 + t) - \frac{1}{6} l n (1 - t + t^{2}) + ↓$ $+ \frac{\sqrt{3}}{4} {t g}^{- 1} (\frac{2 t - 1}{\sqrt{3}}) + \frac{\sqrt[3]{2}}{\sqrt{3}} . \frac{1}{3} l n (1 + t^{3})] + C$ $= \frac{1}{8 A} [4 l n (1 + A x) - 2 l n (1 - A x + A^{2} x^{2}) +$ $+ 3 \sqrt{3} {t g}^{- 1} (\frac{2 A x - 1}{\sqrt{3}}) + \frac{4 \sqrt{3}}{3 A} l n (1 + A^{3} x^{3})] + C .$ $F (1) = \frac{\sqrt[3]{2}}{8} [4 l n (1 + \frac{1}{\sqrt[3]{2}}) - 2 l n (1 - \frac{1}{\sqrt[3]{2}} + \frac{1}{\sqrt[3]{4}}) +$ $+ 3 \sqrt{3} {t g}^{- 1} (\frac{\sqrt[3]{4} - 1}{\sqrt{3}}) + \frac{4 \sqrt[3]{2}}{\sqrt{3}} l n \frac{3}{2}]$ $F (0) = 3 \sqrt{3} {t g}^{- 1} (- \frac{1}{\sqrt{3}}) = - \frac{π \sqrt{3}}{2} .$ $I = F (1) - F (0) = F (1) + \frac{π \sqrt{3}}{2} .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum