Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 142191 by iloveisrael last updated on 27/May/21

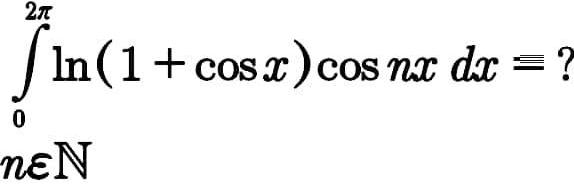
Commented by Mathspace last updated on 27/May/21

$$whytan\left(\frac{x}{2}\right)=i+\frac{2i}{1+e^{ix}}?$$$$andwhatisvalueof{\int }_0^{2\pi }\frac{sin\left(nx\right)}{1+e^{ix}}dx$$$$allthisneedproof...$$

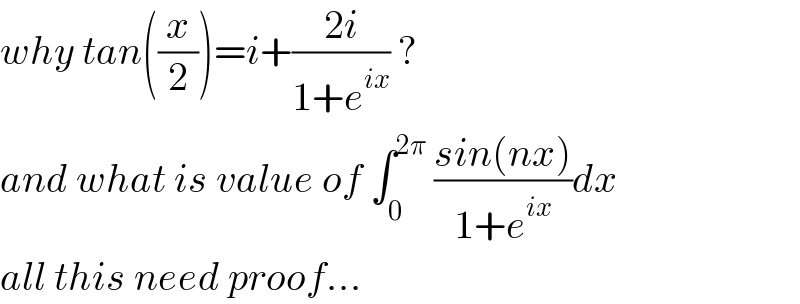
Commented by MJS_new last updated on 28/May/21

$$\mathrm{typo}$$$$\tan \frac{x}{2}=-\mathrm{i}+\frac{2\mathrm{i}}{1+{\mathrm{e}}^{\mathrm{i}x}}$$$$\mathrm{proof}:$$$$\tan y=\frac{\sin y}{\cos y}=\frac{\frac{{\mathrm{e}}^{\mathrm{i}y}-{\mathrm{e}}^{-\mathrm{i}y}}{2\mathrm{i}}}{\frac{{\mathrm{e}}^{\mathrm{i}y}+{\mathrm{e}}^{-\mathrm{i}y}}{2}}=-\mathrm{i}\frac{{\mathrm{e}}^{2\mathrm{i}y}-1}{{\mathrm{e}}^{2\mathrm{i}y}+1}=-\mathrm{i}(1-\frac{2}{{\mathrm{e}}^{2\mathrm{i}y}+1})=$$$$[y=\frac{x}{2}]$$$$=-\mathrm{i}+\frac{2}{1+{\mathrm{e}}^{\mathrm{i}x}}$$

Commented by iloveisrael last updated on 27/May/21

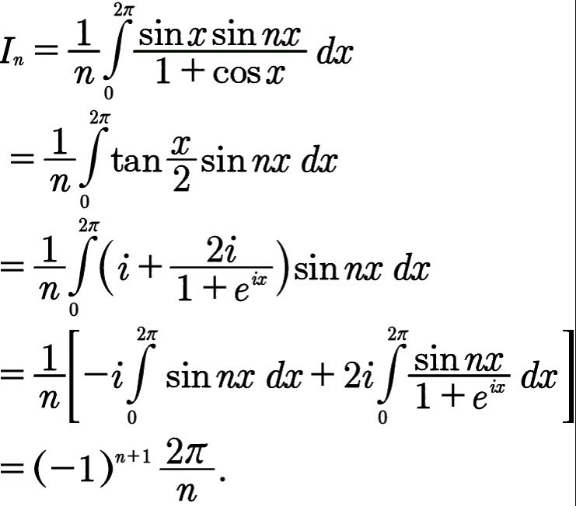
Answered by mathmax by abdo last updated on 28/May/21

$${\mathrm{A}}_{\mathrm{n}}={\int }_0^{2\pi }\log (1+\mathrm{cosx})\cos \left(\mathrm{nx}\right)\mathrm{dx}\mathrm{by}\mathrm{parts}\mathrm{we}\mathrm{get}$$$${\mathrm{A}}_{\mathrm{n}}={\left[\frac{1}{\mathrm{n}}\sin \left(\mathrm{nx}\right)\log (1+\mathrm{cosx})\right]}_0^{2\pi }-{\int }_0^{2\pi }\frac{1}{\mathrm{n}}\sin \left(\mathrm{nx}\right)\times \frac{-\mathrm{sinx}}{1+\mathrm{cosx}}\mathrm{dx}$$$$=\frac{1}{\mathrm{n}}{\int }_0^{2\pi }\frac{\mathrm{sinx}.\sin \left(\mathrm{nx}\right)}{1+\mathrm{cosx}}\mathrm{dx}\Rightarrow {\mathrm{nA}}_{\mathrm{n}}={\int }_0^{2\pi }\frac{\mathrm{sinx}.\sin \left(\mathrm{nx}\right)}{1+\mathrm{cosx}}\mathrm{dx}$$$$={\int }_0^{2\pi }\frac{{\mathrm{e}}^{\mathrm{ix}}-{\mathrm{e}}^{-\mathrm{ix}}}{2\mathrm{i}}.\frac{{\mathrm{e}}^{\mathrm{inx}}-{\mathrm{e}}^{-\mathrm{inx}}}{2\mathrm{i}}.\frac{1}{1+\frac{{\mathrm{e}}^{\mathrm{ix}}+{\mathrm{e}}^{-\mathrm{ix}}}{2}}\mathrm{dx}$$$$=-\frac{1}{2}{\int }_0^{2\pi }\frac{({\mathrm{e}}^{\mathrm{ix}}-{\mathrm{e}}^{-\mathrm{ix}})({\mathrm{e}}^{\mathrm{inx}}-{\mathrm{e}}^{-\mathrm{inx}})}{2+{\mathrm{e}}^{\mathrm{ix}}+{\mathrm{e}}^{-\mathrm{ix}}}\mathrm{dx}$$$${=}_{{\mathrm{e}}^{\mathrm{ix}}=\mathrm{z}}-\frac{1}{2}{\int }_{\mid \mathrm{z}\mid =1}\frac{(\mathrm{z}-{\mathrm{z}}^{-1})({\mathrm{z}}^{\mathrm{n}}-{\mathrm{z}}^{-\mathrm{n}})}{(2+\mathrm{z}+{\mathrm{z}}^{-1})}\frac{\mathrm{dz}}{\mathrm{iz}}$$$$=\frac{\mathrm{i}}{2}{\int }_{\mid \mathrm{z}\mid =1}\frac{{\mathrm{z}}^{\mathrm{n}+1}-{\mathrm{z}}^{-\mathrm{n}+1}-{\mathrm{z}}^{\mathrm{n}-1}-{\mathrm{z}}^{-\mathrm{n}-1}}{{(\mathrm{z}+1)}^2}\mathrm{dz}$$$$=\frac{\mathrm{i}}{2}\left(2\mathrm{i}\pi \right)\mathrm{Res}(\phi ,-1)\mathrm{with}\phi \left(\mathrm{z}\right)=\frac{{\mathrm{z}}^{\mathrm{n}+1}-{\mathrm{z}}^{-\mathrm{n}+1}-{\mathrm{z}}^{\mathrm{n}-1}-{\mathrm{z}}^{-\mathrm{n}-1}}{{(\mathrm{z}+1)}^2}$$$${\mathrm{Res}(\phi ,-1)={\lim }_{\mathrm{z}\to -1}\frac{1}{(2-1)!}\left\{{(\mathrm{z}+1)}^2\right\}\phi \left(\mathrm{z}\right)\}}^{\left(1\right)}$$$$={\lim }_{\mathrm{z}\to -1}{\{{\mathrm{z}}^{\mathrm{n}+1}-{\mathrm{z}}^{-\mathrm{n}+1}-{\mathrm{z}}^{\mathrm{n}-1}-{\mathrm{z}}^{-\mathrm{n}-1}\}}^{\left(1\right)}$$$$={\lim }_{\mathrm{z}\to -1}(\mathrm{n}+1){\mathrm{z}}^{\mathrm{n}}-(-\mathrm{n}+1){\mathrm{z}}^{-\mathrm{n}}-(\mathrm{n}-1){\mathrm{z}}^{\mathrm{n}-2}+(\mathrm{n}+1){\mathrm{z}}^{-\mathrm{n}-2}$$$$=(\mathrm{n}+1){(-1)}^{\mathrm{n}}+(\mathrm{n}-1){(-1)}^{\mathrm{n}}-(\mathrm{n}-1){(-1)}^{\mathrm{n}}+(\mathrm{n}+1){(-1)}^{\mathrm{n}}$$$$={(-1)}^{\mathrm{n}}\{\mathrm{n}+1+\mathrm{n}-1-\mathrm{n}+1+\mathrm{n}+1\}$$$$=(2\mathrm{n}+2){(-1)}^{\mathrm{n}}\Rightarrow {\mathrm{nA}}_{\mathrm{n}}=-\pi (2\mathrm{n}+2){(-1)}^{\mathrm{n}}\Rightarrow$$$${\mathrm{A}}_{\mathrm{n}}=\frac{2\pi (\mathrm{n}+1){(-1)}^{\mathrm{n}-1}}{\mathrm{n}}(\mathrm{n}⩾1)$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com