
Question and Answers Forum
Question Number 142717 by mohammad17 last updated on 04/Jun/21

Commented by mohammad17 last updated on 04/Jun/21
Answered by Ar Brandon last updated on 04/Jun/21
Answered by MJS_new last updated on 04/Jun/21
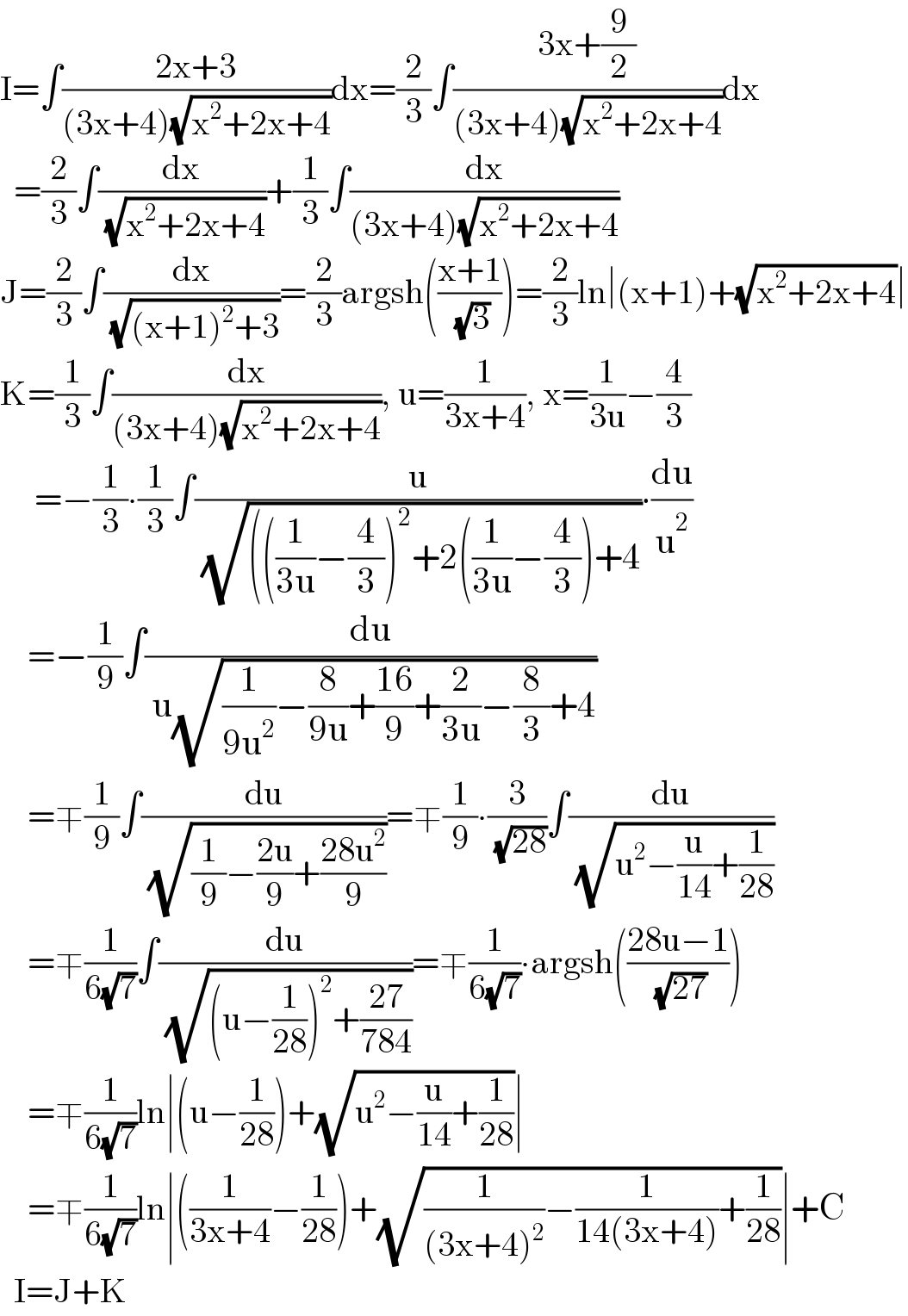
![((2x+3)/(3x+4))=(2/3)+(1/(3(3x+4))) ∫((2x+3)/((3x+4)(√(x^2 +2x+4))))dx= =(2/3)∫(dx/( (√(x^2 +2x+4))))+(1/3)∫(dx/((3x+4)(√(x^2 +2x+4))))= [t=x+1 → dx=dt] =(2/3)∫(dt/( (√(t^2 +3))))+(1/3)∫(dt/((3t+1)(√(t^2 +3))))= [u=((t+(√(t^2 +3)))/( (√3))) → dt=((√(3(t^2 +3)))/(t+(√(t^2 +3))))du=((√(t^2 +3))/u)du] (usually you would now substitute t=(√3)sinh u but I don′t like dealing with hyperbolic functions) =(2/3)∫(du/u)+((2(√3))/(27))∫(du/(u^2 +((2(√3))/9)u−1))= [v=u+((√3)/9) → du=dv] =(2/3)ln u +((2(√3))/(27))∫(dv/(v^2 −((28)/(27))))= [w=((3(√(21)))/(14))v → dv=((2(√(21)))/9)dw] =(2/3)ln u +((√7)/(21))∫(dw/(w^2 −1))= =(2/3)ln u +((√7)/(42))ln ((w−1)/(w+1)) = ... =(2/3)ln (x+1+(√(x^2 +2x+4))) +((√7)/(42))ln ∣((x−8+2(√(7(x^2 +2x+4))))/(3x+4))∣ +C](Q142731.png)
| ||
Question and Answers Forum | ||
Question Number 142717 by mohammad17 last updated on 04/Jun/21 | ||
 | ||
Commented by mohammad17 last updated on 04/Jun/21 | ||
 | ||
Answered by Ar Brandon last updated on 04/Jun/21 | ||
 | ||
| ||
Answered by MJS_new last updated on 04/Jun/21 | ||
![((2x+3)/(3x+4))=(2/3)+(1/(3(3x+4))) ∫((2x+3)/((3x+4)(√(x^2 +2x+4))))dx= =(2/3)∫(dx/( (√(x^2 +2x+4))))+(1/3)∫(dx/((3x+4)(√(x^2 +2x+4))))= [t=x+1 → dx=dt] =(2/3)∫(dt/( (√(t^2 +3))))+(1/3)∫(dt/((3t+1)(√(t^2 +3))))= [u=((t+(√(t^2 +3)))/( (√3))) → dt=((√(3(t^2 +3)))/(t+(√(t^2 +3))))du=((√(t^2 +3))/u)du] (usually you would now substitute t=(√3)sinh u but I don′t like dealing with hyperbolic functions) =(2/3)∫(du/u)+((2(√3))/(27))∫(du/(u^2 +((2(√3))/9)u−1))= [v=u+((√3)/9) → du=dv] =(2/3)ln u +((2(√3))/(27))∫(dv/(v^2 −((28)/(27))))= [w=((3(√(21)))/(14))v → dv=((2(√(21)))/9)dw] =(2/3)ln u +((√7)/(21))∫(dw/(w^2 −1))= =(2/3)ln u +((√7)/(42))ln ((w−1)/(w+1)) = ... =(2/3)ln (x+1+(√(x^2 +2x+4))) +((√7)/(42))ln ∣((x−8+2(√(7(x^2 +2x+4))))/(3x+4))∣ +C](Q142731.png) | ||
| ||