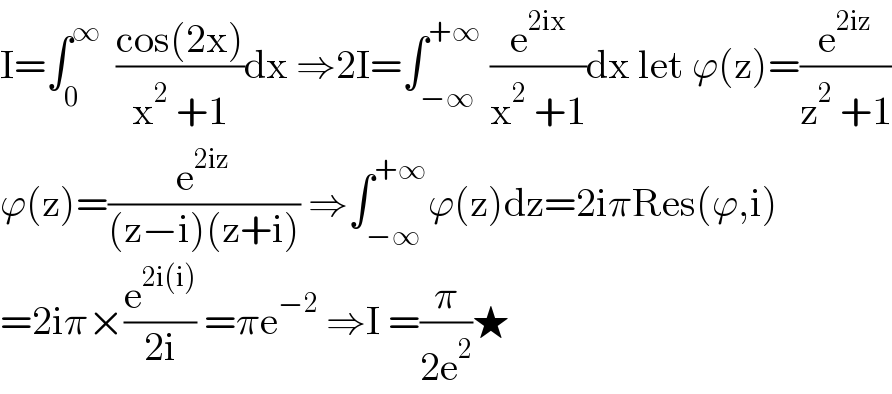Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 148064 by tabata last updated on 25/Jul/21

Commented by tabata last updated on 25/Jul/21

$$helpmesirincomplexnumber$$

Answered by Olaf_Thorendsen last updated on 25/Jul/21

$$\mathrm{Q}6.$$$$\mathrm{I}={\int }_0^{\pi }\frac{d\theta }{2-\cos \theta }$$$$\mathrm{Let}t=\tan \frac{\theta }{2}$$$$\mathrm{I}={\int }_0^{\mathrm{\infty }}\frac{1}{2-\frac{1-t^2}{1+t^2}}.\frac{2dt}{1+t^2}$$$$\mathrm{I}=2{\int }_0^{\mathrm{\infty }}\frac{dt}{2(1+t^2)-(1-t^2)}$$$$\mathrm{I}=2{\int }_0^{\mathrm{\infty }}\frac{dt}{3t^2+1}=\frac{2}{\sqrt{3}}{\int }_0^{\mathrm{\infty }}\frac{\sqrt{3}dt}{3t^2+1}$$$$\mathrm{I}=\frac{2}{\sqrt{3}}{\left[\arctan \left(\sqrt{3}t\right)\right]}_0^{\mathrm{\infty }}=\frac{\pi }{\sqrt{3}}$$

Answered by Olaf_Thorendsen last updated on 25/Jul/21

$$\mathrm{J}={\int }_0^{\mathrm{\infty }}\frac{\cos \left(2x\right)}{x^2+1}dx=\frac{1}{2}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\cos \left(2x\right)}{x^2+1}dx$$$$\mathrm{J}=\frac{1}{2}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{e^{2ix}}{x^2+1}dx$$$$\mathrm{J}=\frac{1}{2}.(2i\pi .\mathrm{Res}(\frac{e^{2ix}}{x^2+1},+i))$$$$\mathrm{J}=i\pi .\underset{x\to +i}{\lim }\left(\frac{e^{2ix}}{x+i}\right)=i\pi .\frac{e^{-2}}{2i}=\frac{\pi }{2e^2}$$

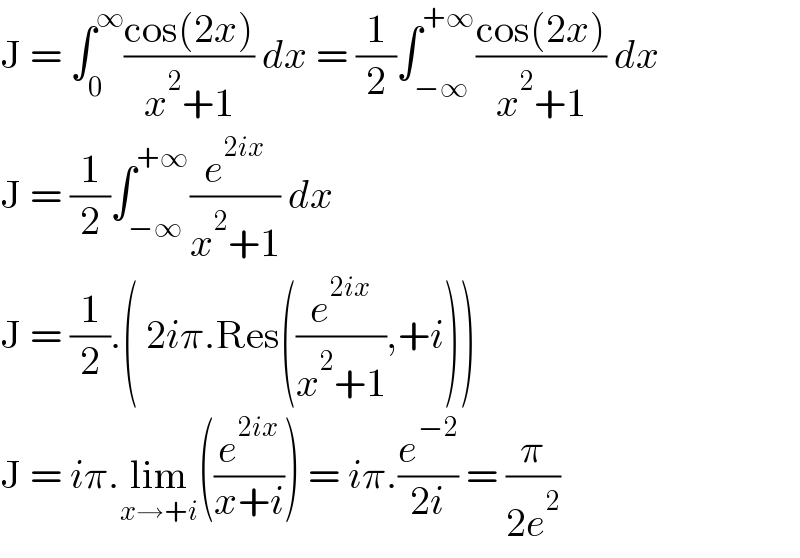
Answered by qaz last updated on 25/Jul/21

$${\int }_0^{\mathrm{\infty }}\frac{\mathcal{L}\left\{\cos \left(\mathrm{ax}\right)\right\}}{{\mathrm{x}}^2+1}\mathrm{dx}={\int }_0^{\mathrm{\infty }}\frac{\mathrm{s}}{({\mathrm{x}}^2+1)({\mathrm{x}}^2+{\mathrm{s}}^2)}\mathrm{dx}=\frac{\pi }{2(\mathrm{s}+1)}$$$${\int }_0^{\mathrm{\infty }}\frac{\cos \left(2\mathrm{x}\right)}{{\mathrm{x}}^2+1}\mathrm{dx}={\mathcal{L}}^{-1}\left\{\frac{\pi }{2(\mathrm{s}+1)}\right\}(\mathrm{a}=2)=\frac{\pi }{{2\mathrm{e}}^2}$$

Answered by mathmax by abdo last updated on 25/Jul/21

$$\mathrm{I}={\int }_0^{\mathrm{\infty }}\frac{\cos \left(2\mathrm{x}\right)}{{\mathrm{x}}^2+1}\mathrm{dx}\Rightarrow 2\mathrm{I}={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{{\mathrm{e}}^{2\mathrm{ix}}}{{\mathrm{x}}^2+1}\mathrm{dx}\mathrm{let}\phi \left(\mathrm{z}\right)=\frac{{\mathrm{e}}^{2\mathrm{iz}}}{{\mathrm{z}}^2+1}$$$$\phi \left(\mathrm{z}\right)=\frac{{\mathrm{e}}^{2\mathrm{iz}}}{(\mathrm{z}-\mathrm{i})(\mathrm{z}+\mathrm{i})}\Rightarrow {\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\phi \left(\mathrm{z}\right)\mathrm{dz}=2\mathrm{i}\pi \mathrm{Res}(\phi ,\mathrm{i})$$$$=2\mathrm{i}\pi \times \frac{{\mathrm{e}}^{2\mathrm{i}\left(\mathrm{i}\right)}}{2\mathrm{i}}=\pi {\mathrm{e}}^{-2}\Rightarrow \mathrm{I}=\frac{\pi }{{2\mathrm{e}}^2}★$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com