Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 150944 by ajfour last updated on 16/Aug/21

Commented by mr W last updated on 17/Aug/21

Commented by ajfour last updated on 17/Aug/21
okay find minimum side length, sir.
Commented by mr W last updated on 17/Aug/21

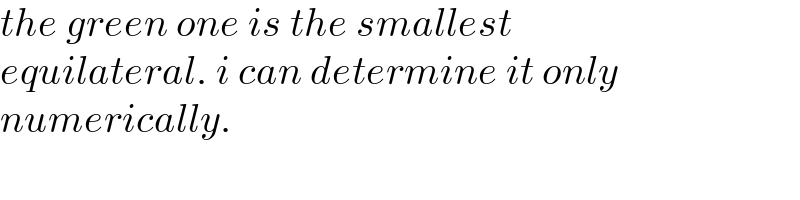
$t h e g r e e n o n e i s t h e s m a l l e s t$ $e q u i l a t e r a l . i c a n d e t e r m i n e i t o n l y$ $n u m e r i c a l l y .$
	Answered by ajfour last updated on 17/Aug/21
	$sin α=(a/(b−a)) A[(√((b−a)^2 −a^2 )), a]≡[c,a] let T(p,q) let s be circumradius of such an equilateral triangle. P[p−scos θ, q+ssin θ] Q[p+scos (60°−θ), q+ssin (60°−θ)] R[p+scos (60°+θ), q−ssin (60°+θ)] now (p−scos θ−c)^2 +(q+ssin θ−a)^2 = a^2 ...(i) [p+scos (60°−θ)]^2 +[q+ssin (60°−θ)]^2 = b^2 ...(ii) q=ssin (60°+θ) ⇒ (p−scos θ−c)^2 +[((s(√3))/2)cos θ+((3s)/2)sin θ−a]^2 =a^2 ........(I) [p+(s/2)cos θ+((s(√3))/2)sin θ]^2 +[s(√3)cos θ]^2 =b^2 ....(II) (II)−(I) {((3s)/2)cos θ+((s(√3))/2)sin θ+c} ×{2p−(s/2)cos θ+((s(√3))/2)sin θ−c} + {((s(√3))/2)cos θ−((3s)/2)sin θ+a} ×{((3(√3)s)/2)cos θ+((3s)/2)sin θ−a} = b^2 −a^2 from here p=f(s,θ) now using (I) or (II) h(s,θ)=0 from here we get s_(min) . Minimum side length of such an equilateral △ would then be s_(min) (√3).$
	$\sin α = \frac{a}{b - a}$ $A [\sqrt{{(b - a)}^{2} - a^{2}}, a] \equiv [c, a]$ $l e t T (p, q)$ $l e t s b e c i r c u m r a d i u s o f s u c h a n$ $e q u i l a t e r a l t r i a n g l e .$ $P [p - s \cos θ, q + s \sin θ]$ $Q [p + s \cos (60 ° - θ), q + s \sin (60 ° - θ)]$ $R [p + s \cos (60 ° + θ), q - s \sin (60 ° + θ)]$ $n o w$ ${(p - s \cos θ - c)}^{2} + {(q + s \sin θ - a)}^{2}$ $= a^{2} . . . (i)$ ${[p + s \cos (60 ° - θ)]}^{2} + {[q + s \sin (60 ° - θ)]}^{2}$ $= b^{2} . . . (i i)$ $q = s \sin (60 ° + θ)$ $\Rightarrow {(p - s \cos θ - c)}^{2}$ $+ {[\frac{s \sqrt{3}}{2} \cos θ + \frac{3 s}{2} \sin θ - a]}^{2} = a^{2}$ $. . . . . . . . (I)$ ${[p + \frac{s}{2} \cos θ + \frac{s \sqrt{3}}{2} \sin θ]}^{2}$ $+ {[s \sqrt{3} \cos θ]}^{2} = b^{2} . . . . (I I)$ $(I I) - (I)$ ${\frac{3 s}{2} \cos θ + \frac{s \sqrt{3}}{2} \sin θ + c}$ $\times {2 p - \frac{s}{2} \cos θ + \frac{s \sqrt{3}}{2} \sin θ - c}$ $+$ ${\frac{s \sqrt{3}}{2} \cos θ - \frac{3 s}{2} \sin θ + a}$ $\times {\frac{3 \sqrt{3} s}{2} \cos θ + \frac{3 s}{2} \sin θ - a}$ $= b^{2} - a^{2}$ $f r o m h e r e$ $p = f (s, θ)$ $n o w u s i n g (I) o r (I I)$ $h (s, θ) = 0$ $f r o m h e r e w e g e t s_{m i n} .$ $M i n i m u m s i d e l e n g t h o f$ $s u c h a n e q u i l a t e r a l △ w o u l d$ $t h e n b e s_{m i n} \sqrt{3} .$
	Answered by ajfour last updated on 17/Aug/21
	$center of semicircle origin. center of circle A[(√((b−a)^2 −a^2 )), a]≡(c,a) let bottom corner be B(p,0) let side of △ be s. x_C ^2 +y_C ^2 =b^2 (x_C −p)^2 +y_C ^2 =s^2 subtracting 2px_C −p^2 =b^2 −s^2 x_C =((b^2 −s^2 +p^2 )/(2p)) ((x_c +p)/2)−((s(√3))/2)sin φ=x_D (y_C /2)+((s(√3))/2)cos φ=y_D (x_D −c)^2 +(y_D −a)^2 =a^2 cos φ=((x_C −p)/s) ; sin φ=(y_C /s) x_C +p−s(√3)(((√(b^2 −x_C ^2 ))/s))=2x_D y_C +s(√3)(((x_C −p)/s))=2y_D Now {x_C +p−s(√3)((y_C /s))−2c}^2 +{y_C +s(√3)(((x_C −p)/s))−a}^2 =a^2 but x_C =((b^2 −s^2 +p^2 )/(2p)) ; y_C =(√(b^2 −x_C ^2 )) =(√(b^2 −(((b^2 −s^2 +p^2 )/(2p)))^2 )) ⇒ {((b^2 −s^2 +p^2 )/(2p))+p−(√3)(√(b^2 −(((b^2 −s^2 +p^2 )/(2p)))^2 ))−2c}^2 +{(√(b^2 −(((b^2 −s^2 +p^2 )/(2p)))^2 ))+(√3)(((b^2 −s^2 +p^2 )/(2p)))−(√3)p−a}^2 =a^2 eq. is implicit in s and p. we can graph it and can find the s_(min) .$
	$c e n t e r o f s e m i c i r c l e o r i g i n .$ $c e n t e r o f c i r c l e$ $A [\sqrt{{(b - a)}^{2} - a^{2}}, a] \equiv (c, a)$ $l e t b o t t o m c o r n e r b e B (p, 0)$ $l e t s i d e o f △ b e s .$ $x_{C}^{2} + y_{C}^{2} = b^{2}$ ${(x_{C} - p)}^{2} + y_{C}^{2} = s^{2}$ $s u b t r a c t i n g$ $2 {p x}_{C} - p^{2} = b^{2} - s^{2}$ $x_{C} = \frac{b^{2} - s^{2} + p^{2}}{2 p}$ $\frac{x_{c} + p}{2} - \frac{s \sqrt{3}}{2} \sin ϕ = x_{D}$ $\frac{y_{C}}{2} + \frac{s \sqrt{3}}{2} \cos ϕ = y_{D}$ ${(x_{D} - c)}^{2} + {(y_{D} - a)}^{2} = a^{2}$ $\cos ϕ = \frac{x_{C} - p}{s}; \sin ϕ = \frac{y_{C}}{s}$ $x_{C} + p - s \sqrt{3} (\frac{\sqrt{b^{2} - x_{C}^{2}}}{s}) = 2 x_{D}$ $y_{C} + s \sqrt{3} (\frac{x_{C} - p}{s}) = 2 y_{D}$ $N o w$ ${x_{C} + p - s \sqrt{3} (\frac{y_{C}}{s}) - 2 c}^{2}$ $+ {y_{C} + s \sqrt{3} (\frac{x_{C} - p}{s}) - a}^{2} = a^{2}$ $b u t x_{C} = \frac{b^{2} - s^{2} + p^{2}}{2 p};$ $y_{C} = \sqrt{b^{2} - x_{C}^{2}}$ $= \sqrt{b^{2} - {(\frac{b^{2} - s^{2} + p^{2}}{2 p})}^{2}}$ $\Rightarrow$ ${\frac{b^{2} - s^{2} + p^{2}}{2 p} + p - \sqrt{3} \sqrt{b^{2} - {(\frac{b^{2} - s^{2} + p^{2}}{2 p})}^{2}} - 2 c}^{2}$ $+ {\sqrt{b^{2} - {(\frac{b^{2} - s^{2} + p^{2}}{2 p})}^{2}} + \sqrt{3} (\frac{b^{2} - s^{2} + p^{2}}{2 p}) - \sqrt{3} p - a}^{2} = a^{2}$ $e q . i s i m p l i c i t i n s a n d p .$ $w e c a n g r a p h i t a n d c a n f i n d$ $t h e s_{m i n} .$
	Commented by mr W last updated on 17/Aug/21

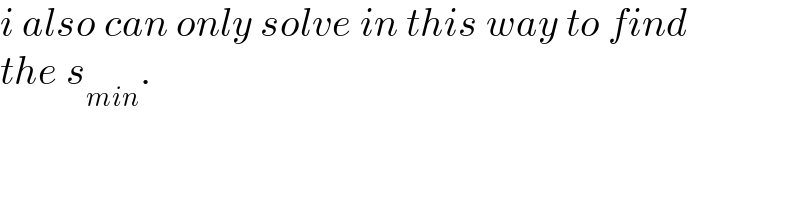
	$i a l s o c a n o n l y s o l v e i n t h i s w a y t o f i n d$ $t h e s_{m i n} .$
	Answered by ajfour last updated on 17/Aug/21
	$O(center of semicircle) z_A =(√((b−a)^2 −a^2 ))+ia=c+ia z_B =p z_C =p+s(cos θ+isin θ) z_D =p+s[−cos (((2π)/3)−θ)+isin (((2π)/3)−θ)] ∣z_D −z_A ∣=a ∣z_C ∣=b (p+scos θ)^2 +s^2 sin^2 θ=b^2 ⇒ p^2 +2spcos θ+s^2 =b^2 ....(i) {p+scos (((2π)/3)−θ)−c}^2 +{ssin (((2π)/3)−θ)−a}^2 =a^2 ..(ii) say ((2π)/3)−θ=φ , then ⇒ p^2 +s^2 +c^2 +2spcos φ =2cp+2cscos φ+2assin φ ⇒ b^2 +2sp(cos φ−cos θ)+c^2 = 2cp+2s(ccos φ+asin φ) p=((b^2 +c^2 −2s(ccos φ+asin φ))/(2c−2s(cos φ−cos θ))) using this in p^2 +2spcos θ+s^2 =b^2 ....(i) ⇒ {((b^2 +c^2 −2s(ccos φ+asin φ))/(2c−2s(cos φ−cos θ)))+scos θ}^2 +s^2 sin^2 θ=b^2 ⇒ {((b^2 +c^2 −2s[c+atan (((2π)/3)−θ)])/(2c−2s[1−((cos θ)/(cos (((2π)/3)−θ)))]))+scos θ}^2 +s^2 sin^2 θ=b^2 for a=2, b=5 c=(√5) {((30−2s[(√5)+2tan (((2π)/3)−θ)])/(2(√5)−2s[1−((cos θ)/(cos (((2π)/3)−θ)))]))+scos θ}^2 +s^2 sin^2 θ=25 {((30−2s(√5)−2s((((√3)cos θ−sin θ)/(cos θ−(√3)sin θ))))/(2(√5)−2s+4s(((cos θ)/( (√3)sin θ+cos θ)))))+scos θ}^2 +s^2 sin^2 θ=25 graph of this f(s,θ)=25 should give s_(min) . sir can u help?$
	$O (c e n t e r o f s e m i c i r c l e)$ $z_{A} = \sqrt{{(b - a)}^{2} - a^{2}} + i a = c + i a$ $z_{B} = p$ $z_{C} = p + s (\cos θ + i \sin θ)$ $z_{D} = p + s [- \cos (\frac{2 π}{3} - θ) + i \sin (\frac{2 π}{3} - θ)]$ $∣ z_{D} - z_{A} ∣= a$ $∣ z_{C} ∣= b$ ${(p + s \cos θ)}^{2} + s^{2} \sin^{2} θ = b^{2}$ $\Rightarrow$ $p^{2} + 2 s p \cos θ + s^{2} = b^{2} . . . . (i)$ ${p + s \cos (\frac{2 π}{3} - θ) - c}^{2}$ $+ {s \sin (\frac{2 π}{3} - θ) - a}^{2} = a^{2} . . (i i)$ $s a y \frac{2 π}{3} - θ = ϕ, t h e n$ $\Rightarrow p^{2} + s^{2} + c^{2} + 2 s p \cos ϕ$ $= 2 c p + 2 c s \cos ϕ + 2 a s \sin ϕ$ $\Rightarrow b^{2} + 2 s p (\cos ϕ - \cos θ) + c^{2}$ $= 2 c p + 2 s (c \cos ϕ + a \sin ϕ)$ $p = \frac{b^{2} + c^{2} - 2 s (c \cos ϕ + a \sin ϕ)}{2 c - 2 s (\cos ϕ - \cos θ)}$ $u s i n g t h i s i n$ $p^{2} + 2 s p \cos θ + s^{2} = b^{2} . . . . (i)$ $\Rightarrow$ ${\frac{b^{2} + c^{2} - 2 s (c \cos ϕ + a \sin ϕ)}{2 c - 2 s (\cos ϕ - \cos θ)} + s \cos θ}^{2}$ $+ s^{2} \sin^{2} θ = b^{2}$ $\Rightarrow$ ${\frac{b^{2} + c^{2} - 2 s [c + a \tan (\frac{2 π}{3} - θ)]}{2 c - 2 s [1 - \frac{\cos θ}{\cos (\frac{2 π}{3} - θ)}]} + s \cos θ}^{2}$ $+ s^{2} \sin^{2} θ = b^{2}$ $f o r a = 2, b = 5$ $c = \sqrt{5}$ ${\frac{30 - 2 s [\sqrt{5} + 2 \tan (\frac{2 π}{3} - θ)]}{2 \sqrt{5} - 2 s [1 - \frac{\cos θ}{\cos (\frac{2 π}{3} - θ)}]} + s \cos θ}^{2}$ $+ s^{2} \sin^{2} θ = 25$ ${\frac{30 - 2 s \sqrt{5} - 2 s (\frac{\sqrt{3} \cos θ - \sin θ}{\cos θ - \sqrt{3} \sin θ})}{2 \sqrt{5} - 2 s + 4 s (\frac{\cos θ}{\sqrt{3} \sin θ + \cos θ})} + s \cos θ}^{2}$ $+ s^{2} \sin^{2} θ = 25$ $g r a p h o f t h i s f (s, θ) = 25$ $s h o u l d g i v e s_{m i n} .$ $s i r c a n u h e l p ?$
	Answered by mr W last updated on 17/Aug/21

	Commented by mr W last updated on 18/Aug/21

	$s = s i d e l e n g t h o f t r i a n g l e$ $O C = c = \sqrt{{(b - a)}^{2} - a^{2}} = \sqrt{b (b - 2 a)}$ $s a y A (u, 0)$ $u = c - s \cos θ + \sqrt{b^{2} - s^{2} \sin^{2} θ}$ $e q n . o f s m a l l c i r c l e :$ $x^{2} + {(y - a)}^{2} = a^{2}$ $x_{D} = u + s \cos (\frac{π}{3} + θ)$ $y_{D} = s \sin (\frac{π}{3} + θ)$ ${(u + s \cos (\frac{π}{3} + θ))}^{2} + {(s \sin (\frac{π}{3} + θ) - a)}^{2} = a^{2}$ $u^{2} + 2 s u \cos (\frac{π}{3} + θ) + s^{2} - 2 a s \sin (\frac{π}{3} + θ) = 0$ $u = - s \cos (\frac{π}{3} + θ) + \sqrt{s (2 a - s \sin (\frac{π}{3} + θ)) \sin (\frac{π}{3} + θ)}$ $c - s \cos θ + \sqrt{b^{2} - s^{2} \sin^{2} θ} = - s \cos (\frac{π}{3} + θ) + \sqrt{s (2 a - s \sin (\frac{π}{3} + θ)) \sin (\frac{π}{3} + θ)}$ $\Rightarrow s [\cos θ - \cos (\frac{π}{3} + θ)] - \sqrt{b^{2} - s^{2} \sin^{2} θ} + \sqrt{s [2 a - s \sin (\frac{π}{3} + θ)] \sin (\frac{π}{3} + θ)} = c$ $λ [\cos θ - \cos (\frac{π}{3} + θ)] - \sqrt{1 - λ^{2} \sin^{2} θ} + \sqrt{λ [μ - λ \sin (\frac{π}{3} + θ)] \sin (\frac{π}{3} + θ)} = \sqrt{1 - μ}$ $w i t h μ = \frac{2 a}{b} ⩽ 1, λ = \frac{s}{b}$ $f r o m t h i s r e l a t i o n s h i p b e t w e e n s a n d$ $θ w e c a n f i n d t h e s_{m i n} g r a p h i c a l l y .$ $e x a m p l e : a = 2, b = 5$ $s_{m i n} = 3.8157 a t θ = 1.4075 (80.64 °)$
	Commented by mr W last updated on 17/Aug/21

	Commented by mr W last updated on 17/Aug/21

	Commented by mr W last updated on 17/Aug/21

	Commented by mr W last updated on 18/Aug/21

	Commented by mr W last updated on 18/Aug/21

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum