Math Question and Answers


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 151636 by Tawa11 last updated on 22/Aug/21

Commented by mr W last updated on 22/Aug/21
$do you know the psi−function and ψ(1+z)=−γ+Σ_(n=1) ^∞ ((1/n)−(1/(n+z))) ? if not, then you should learn this at first. Σ_(n=0) ^∞ (1/((n+α)(n+β))) =(1/(β−α))Σ_(n=0) ^∞ [(1/(n+α))−(1/(n+β))] =(1/(β−α)){Σ_(n=0) ^∞ [(1/(n+α))]−Σ_(n=0) ^∞ [(1/(n+β))]} =(1/(β−α)){Σ_(n=1) ^∞ [(1/(n+(α−1)))]−Σ_(n=1) ^∞ [(1/(n+(β−1)))]} =(1/(β−α)){−γ+Σ_(n=1) ^∞ (1/n)−ψ(1+(α−1))−[−γ+Σ_(n=1) ^∞ (1/n)−ψ(1+(β−1))]} =(1/(β−α)){ψ(β)−ψ(α)}$
$d o y o u k n o w t h e p s i - f u n c t i o n a n d$ $ψ (1 + z) = - γ + \underset{n = 1}{\sum^{\infty}} (\frac{1}{n} - \frac{1}{n + z}) ?$ $i f n o t, t h e n y o u s h o u l d l e a r n t h i s a t$ $f i r s t .$ $\underset{n = 0}{\sum^{\infty}} \frac{1}{(n + α) (n + β)}$ $= \frac{1}{β - α} \underset{n = 0}{\sum^{\infty}} [\frac{1}{n + α} - \frac{1}{n + β}]$ $= \frac{1}{β - α} {\underset{n = 0}{\sum^{\infty}} [\frac{1}{n + α}] - \underset{n = 0}{\sum^{\infty}} [\frac{1}{n + β}]}$ $= \frac{1}{β - α} {\underset{n = 1}{\sum^{\infty}} [\frac{1}{n + (α - 1)}] - \underset{n = 1}{\sum^{\infty}} [\frac{1}{n + (β - 1)}]}$ $= \frac{1}{β - α} {- γ + \underset{n = 1}{\sum^{\infty}} \frac{1}{n} - ψ (1 + (α - 1)) - [- γ + \underset{n = 1}{\sum^{\infty}} \frac{1}{n} - ψ (1 + (β - 1))]}$ $= \frac{1}{β - α} {ψ (β) - ψ (α)}$
Commented by Tawa11 last updated on 22/Aug/21

$Please help .$ $Explain how \underset{n = 0}{\sum^{\infty}} \frac{1}{(n + \frac{2}{3}) (n + \frac{4}{3})} = \frac{ψ (\frac{4}{3}) - ψ (\frac{2}{3})}{\frac{4}{3} - \frac{2}{3}}$ $I need the rule please . Explain . Thanks .$
Commented by Tawa11 last updated on 22/Aug/21

$Wow . This is interesting . God bless you sir .$ $Am reading on it . So, I ask the question so that I can read further .$ $Thanks sir . I appreciate .$
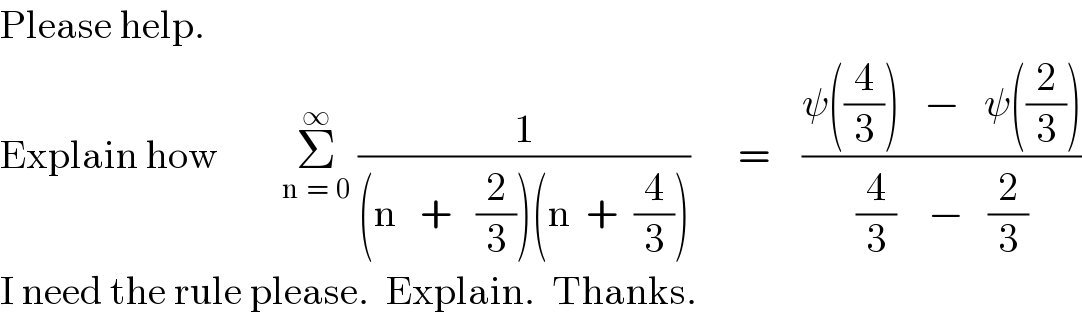
Commented by Tawa11 last updated on 22/Aug/21

$After going through your explanation sir . I understand it perfectly .$ $I am happy . God bless you sir$
	Answered by Olaf_Thorendsen last updated on 22/Aug/21

	$S = \frac{2}{9} \underset{n = 0}{\sum^{\infty}} \frac{1}{(n + \frac{2}{3}) (n + \frac{4}{3})}$ $S = \frac{2}{9} . \frac{ψ (\frac{4}{3}) - ψ (\frac{2}{3})}{\frac{4}{3} - \frac{2}{3}}$ $∙ ψ (z + 1) = ψ (z) + \frac{1}{z}$ $\Rightarrow ψ (\frac{1}{3} + 1) = ψ (\frac{1}{3}) + \frac{1}{1 / 3}$ $ψ (\frac{4}{3}) = ψ (\frac{1}{3}) + 3 (1)$ $∙ ψ (1 - z) - ψ (z) = π \cot (π z)$ $ψ (1 - \frac{1}{3}) - ψ (\frac{1}{3}) = π \cot (\frac{π}{3})$ $ψ (\frac{2}{3}) = ψ (\frac{1}{3}) + \frac{π}{\sqrt{3}} (2)$ $∙ (1) - (2) :$ $ψ (\frac{4}{3}) - ψ (\frac{2}{3}) = 3 - \frac{π}{\sqrt{3}}$ $∙ S = \frac{2}{9} . \frac{3 - \frac{π}{\sqrt{3}}}{\frac{2}{3}} = 1 - \frac{π}{3 \sqrt{3}}$
	Commented by Tawa11 last updated on 22/Aug/21

	$Wow . Thanks sir . I appreciate . God bless you .$ $I am visiting all your solution in the forum on this . Thank you sir .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum