
Question and Answers Forum
Question Number 152980 by mr W last updated on 03/Sep/21

Commented by mathdanisur last updated on 03/Sep/21
![a^7 +b^7 +c^7 = 7abc(ab+bc+ca)^2 a^4 +b^4 +c^4 = 2(ab+bc+ca)^2 S = ((7abc(ab+bc+ca)^2 )/(abc[2(ab+bc+ca)^2 ])) = (7/2) = 3,5](Q152981.png)
Commented by mr W last updated on 03/Sep/21

Commented by mr W last updated on 03/Sep/21
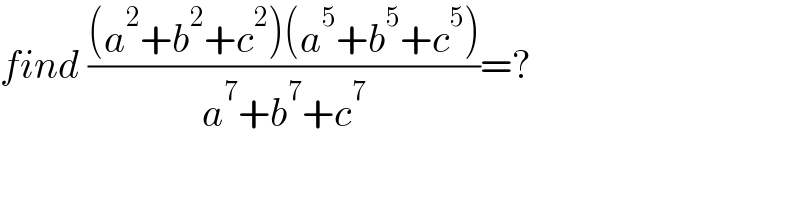
Commented by mathdanisur last updated on 03/Sep/21

Commented by mathdanisur last updated on 03/Sep/21
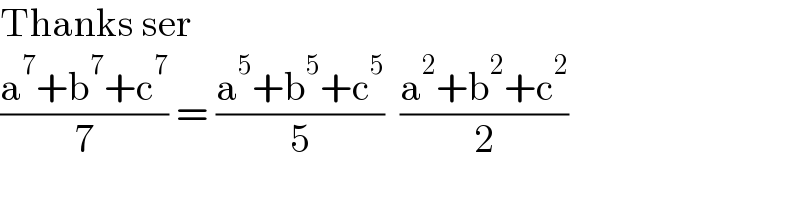
Commented by mathdanisur last updated on 03/Sep/21
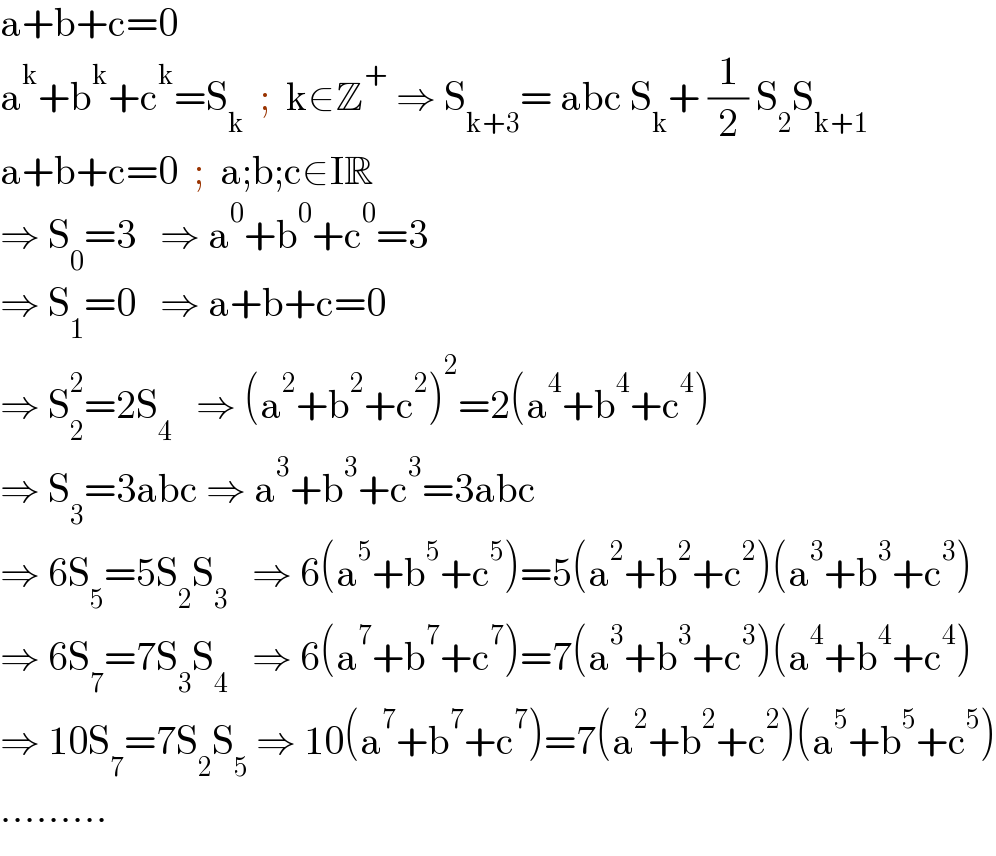
Commented by mathdanisur last updated on 03/Sep/21
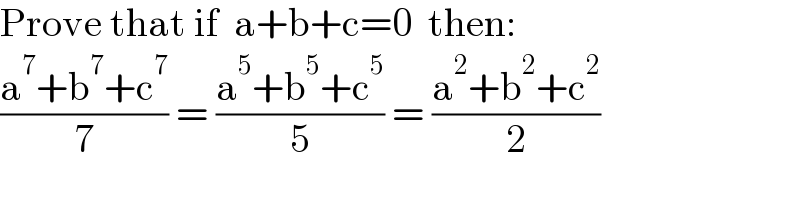
Commented by mr W last updated on 03/Sep/21

Commented by mr W last updated on 03/Sep/21
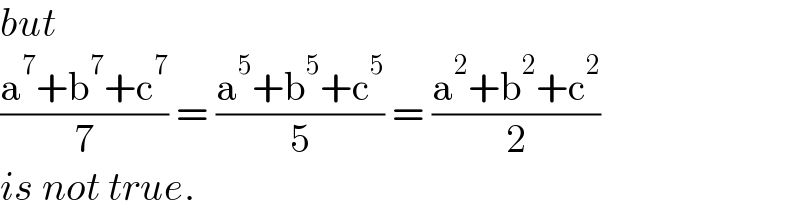
Commented by Tawa11 last updated on 04/Sep/21

Answered by ajfour last updated on 03/Sep/21
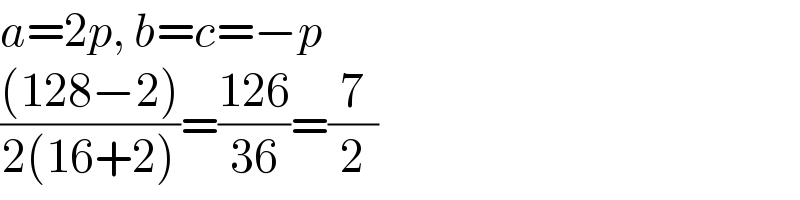
Commented by mr W last updated on 03/Sep/21

Answered by mr W last updated on 04/Sep/21
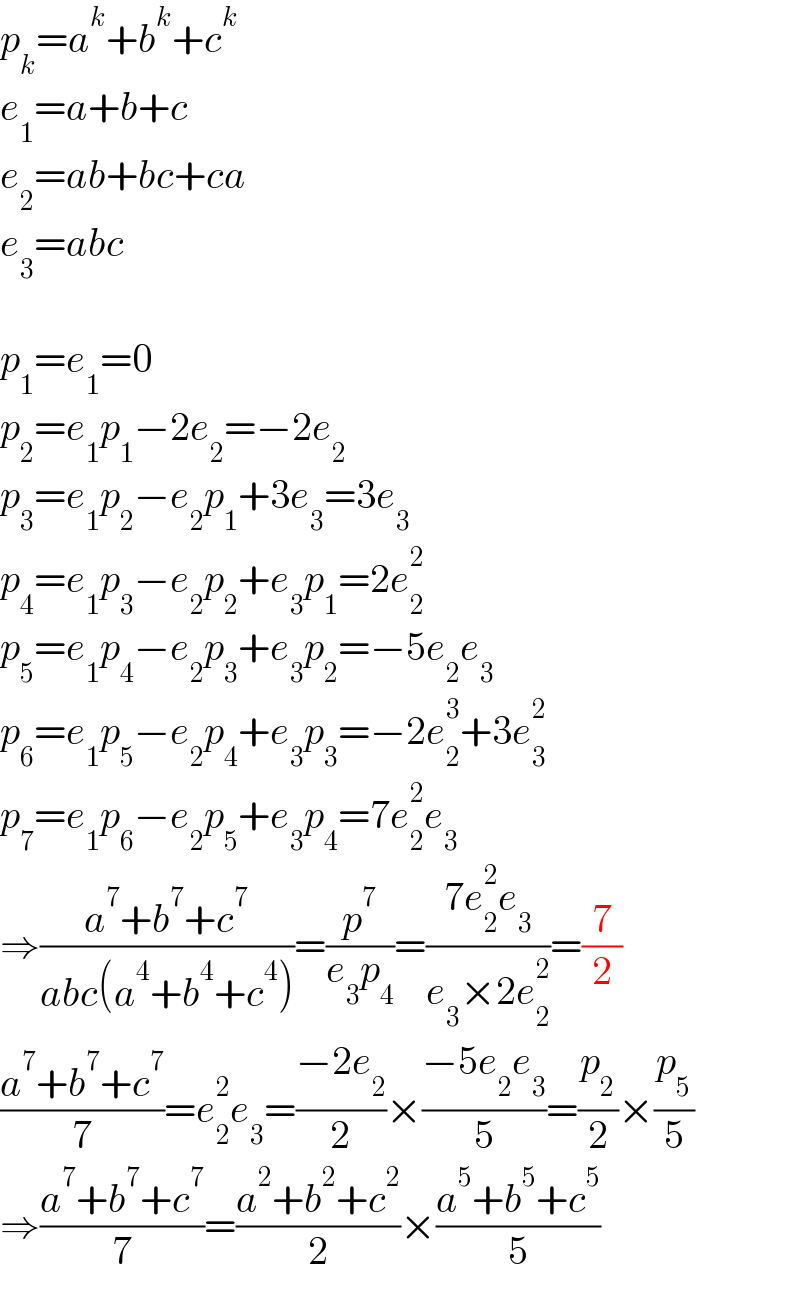
Commented by mathdanisur last updated on 04/Sep/21

