Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 154177 by EDWIN88 last updated on 15/Sep/21

Commented by Tawa11 last updated on 15/Sep/21

$$\mathrm{nice}$$

Commented by EDWIN88 last updated on 16/Sep/21

$$Ptolomeo:$$$$\Rightarrow AB.CD+{CD}^2\sin \alpha \sin \theta ={CD}^2\cos \alpha \cos \theta$$$$\Rightarrow AB=CD(\cos \alpha \cos \theta -\sin \alpha \sin \theta )$$$$\Rightarrow AB=CD\cos (\alpha +\theta )$$

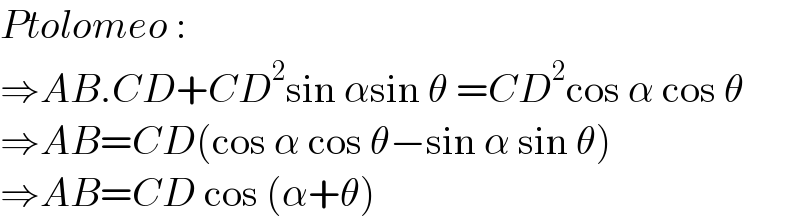
Answered by som(math1967) last updated on 15/Sep/21

Commented by som(math1967) last updated on 15/Sep/21

$$\mathit{l}\mathit{e}\mathit{t}\mathit{o}\mathit{i}\mathit{s}\mathit{c}\mathit{e}\mathit{n}\mathit{t}\mathit{r}\mathit{e}\therefore \mathit{C}\mathit{O}=\mathit{A}\mathit{O}=\mathit{B}\mathit{O}=\frac{\mathit{C}\mathit{D}}{2}$$$$\measuredangle \mathit{B}\mathit{C}\mathit{O}=\measuredangle \mathit{O}\mathit{B}\mathit{C}=\mathit{\theta }[\mathit{C}\mathit{O}=\mathit{B}\mathit{O}]$$$$\therefore \measuredangle \mathit{A}\mathit{B}\mathit{O}=\measuredangle \mathit{B}AO=\mathit{\alpha }+\mathit{\theta }$$$$\measuredangle \mathit{A}\mathit{O}\mathit{B}=180-2(\mathit{\alpha }+\mathit{\theta })$$$$\mathit{f}\mathit{r}\mathit{o}\mathit{m}△\mathit{A}\mathit{O}\mathit{B}$$$$\frac{\mathit{A}\mathit{B}}{\mathit{S}\mathit{i}\mathit{n}(180-2\mathit{\alpha }-2\theta )}=\frac{\mathit{A}\mathit{O}}{\mathit{S}\mathit{i}\mathit{n}(\mathit{\alpha }+\mathit{\theta })}$$$$\frac{\mathit{A}\mathit{B}}{\mathit{S}\mathit{i}\mathit{n}2(\mathit{\alpha }+\mathit{\theta })}=\frac{\mathit{A}\mathit{O}}{\mathit{s}\mathit{i}\mathit{n}(\mathit{\alpha }+\mathit{\theta })}$$$$\frac{\mathit{A}B}{2\mathit{s}\mathit{i}\mathit{n}(\mathit{\alpha }+\theta )c\mathit{o}\mathit{s}(\mathit{\alpha }+\mathit{\theta })}=\frac{\mathit{A}O}{\mathit{s}\mathit{i}\mathit{n}(\mathit{\alpha }+\mathit{\theta })}$$$$\mathit{A}\mathit{B}=2\mathit{A}\mathit{O}\mathit{c}\mathit{o}\mathit{s}(\mathit{\alpha }+\mathit{\theta })$$$$\mathit{A}\mathit{B}=\mathit{C}\mathit{D}\mathit{c}\mathit{o}\mathit{s}(\mathit{\alpha }+\mathit{\theta })\left[\mathit{p}\mathit{r}\mathit{o}\mathit{v}\mathit{e}\mathit{d}\right]$$

Commented by mr W last updated on 15/Sep/21

$$OA=OB=\frac{CD}{2}$$$$AB=2\times OB\cos (\theta +\alpha )=CD\cos (\theta +\alpha )$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com