
Question and Answers Forum
Question Number 154186 by daus last updated on 15/Sep/21
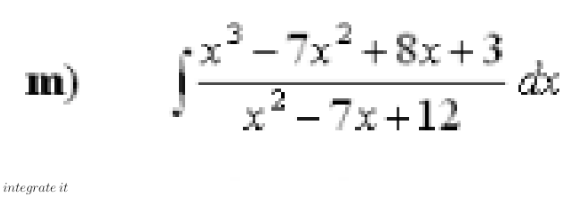
Answered by puissant last updated on 15/Sep/21
![Ω=∫((x^3 −7x^2 +8x+3)/(x^2 −7x+12))dx =∫x−((4x−3)/(x^2 −7x+12))dx = (1/2)x^2 −∫((4x−3)/(x^2 −7x+12))dx =(1/2)x^2 −2∫((2x−(3/2)−((11)/2)+((11)/2))/(x^2 −7x+12))dx =(1/2)x^2 −2∫((2x−7)/(x^2 −7x+12))dx−11∫(dx/(x^2 −7x+12)) =(1/2)x^2 −2ln∣x^2 −7x+12∣−11∫(dx/((x−(7/2))−((49)/4)+12)) =(1/2)x^2 −2ln∣x^2 −7x+12∣−11∫(dx/((1/4)[2(x−(7/2))]^2 +1)) u=2(x−(7/2)) → dx=(du/2) Ω=(1/2)x^2 −2ln∣x^2 −7x+12∣−22∫(du/(1+u^2 )) =(1/2)x^2 −2ln∣x^2 −7x+12∣−22arctan(u)+C.. ∴∵ Ω = (1/2)x^2 −2ln∣x^2 −7x+12∣−22arctan(2x−7)+C..](Q154190.png)
| ||
Question and Answers Forum | ||
Question Number 154186 by daus last updated on 15/Sep/21 | ||
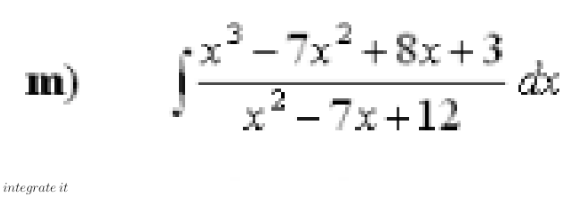 | ||
Answered by puissant last updated on 15/Sep/21 | ||
![Ω=∫((x^3 −7x^2 +8x+3)/(x^2 −7x+12))dx =∫x−((4x−3)/(x^2 −7x+12))dx = (1/2)x^2 −∫((4x−3)/(x^2 −7x+12))dx =(1/2)x^2 −2∫((2x−(3/2)−((11)/2)+((11)/2))/(x^2 −7x+12))dx =(1/2)x^2 −2∫((2x−7)/(x^2 −7x+12))dx−11∫(dx/(x^2 −7x+12)) =(1/2)x^2 −2ln∣x^2 −7x+12∣−11∫(dx/((x−(7/2))−((49)/4)+12)) =(1/2)x^2 −2ln∣x^2 −7x+12∣−11∫(dx/((1/4)[2(x−(7/2))]^2 +1)) u=2(x−(7/2)) → dx=(du/2) Ω=(1/2)x^2 −2ln∣x^2 −7x+12∣−22∫(du/(1+u^2 )) =(1/2)x^2 −2ln∣x^2 −7x+12∣−22arctan(u)+C.. ∴∵ Ω = (1/2)x^2 −2ln∣x^2 −7x+12∣−22arctan(2x−7)+C..](Q154190.png) | ||
| ||