Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 15567 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 11/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 11/Jun/17

$$ABCD\mathrm{\&}MNPQ,aresquares.$$$$showthat:$$$$a^2+b^2=c^2+d^2$$

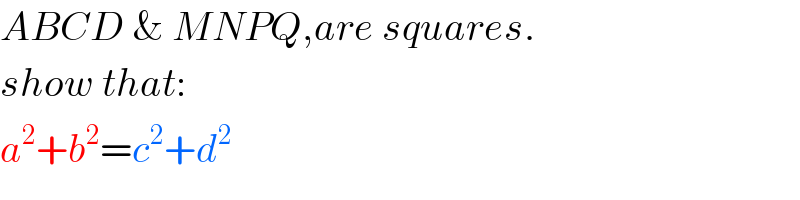
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 13/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 13/Jun/17

$$a^2=s^2+{(p+n\frac{\sqrt{2}}{2})}^2,b^2=q^2+{(r+n\frac{\sqrt{2}}{2})}^2$$$$c^2=p^2+{(q+n\frac{\sqrt{2}}{2})}^2,d^2=r^2+{(s+n\frac{\sqrt{2}}{2})}^2$$$$a^2+b^2=s^2+q^2+p^2+r^2+n^2+2n\sqrt{2}(p+r)\left(i\right)$$$$c^2+d^2=s^2+q^2+p^2+r^2+n^2+2n\sqrt{2}(q+s)\left(ii\right)$$$$q+s++n\sqrt{2}=m,p+r+n\sqrt{2}=m$$$$\Rightarrow p+r=q+s$$$$\left(i\right)-\left(ii\right)\Rightarrow (a^2+b^2)-(c^2+d^2)=0$$$$\Rightarrow {\mathit{a}}^2+{\mathit{b}}^2={\mathit{c}}^2+{\mathit{d}}^2.◼$$

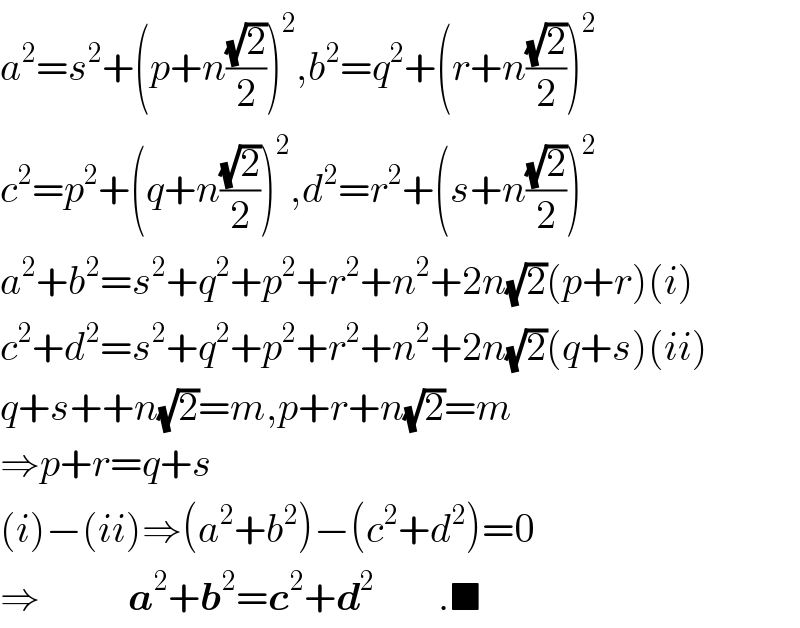
Answered by ajfour last updated on 12/Jun/17

Commented by ajfour last updated on 12/Jun/17

$$let\mathit{s}\cos \theta ={\mathit{s}}_{\mathit{x}},\mathit{s}\sin \theta ={\mathit{s}}_{\mathit{y}}$$$$\mathit{l}isthesideofbiggestsquare$$$$allcomponentsoflengths\mathit{a},\mathit{b},$$$$\mathit{c},\mathit{d},and\mathit{s}arepositive.$$$$fromfigureabove,$$$$c_x=b_x+s_y;c_y=a_y-s_y$$$$d_x=a_x+s_y;d_y=b_y-s_y$$$${\mathit{c}}^2+{\mathit{d}}^2={\mathit{c}}_{\mathit{x}}^2+{\mathit{c}}_{\mathit{y}}^2+{\mathit{d}}_{\mathit{x}}^2+{\mathit{d}}_{\mathit{y}}^2$$$$={({\mathit{b}}_{\mathit{x}}+{\mathit{s}}_{\mathit{y}})}^2+{({\mathit{a}}_{\mathit{y}}-{\mathit{s}}_{\mathit{y}})}^2$$$$+{({\mathit{a}}_{\mathit{x}}+{\mathit{s}}_{\mathit{y}})}^2+{({\mathit{b}}_{\mathit{y}}-{\mathit{s}}_{\mathit{y}})}^2$$$$=({\mathit{a}}_{\mathit{x}}^2+{\mathit{a}}_{\mathit{y}}^2)+({\mathit{b}}_{\mathit{x}}^2+{\mathit{b}}_{\mathit{y}}^2)+4{\mathit{s}}_{\mathit{y}}^2$$$$+2{\mathit{s}}_{\mathit{y}}[({\mathit{a}}_{\mathit{x}}+{\mathit{b}}_{\mathit{x}})-({\mathit{a}}_{\mathit{y}}+{\mathit{b}}_{\mathit{y}})]$$$$Now({\mathit{a}}_{\mathit{x}}+{\mathit{b}}_{\mathit{x}})=\mathit{l}-({\mathit{s}}_{\mathit{x}}+{\mathit{s}}_{\mathit{y}})$$$$and({\mathit{a}}_{\mathit{y}}+{\mathit{b}}_{\mathit{y}})=\mathit{l}-({\mathit{s}}_{\mathit{x}}-{\mathit{s}}_{\mathit{y}})$$$$\Rightarrow ({\mathit{a}}_{\mathit{x}}+{\mathit{b}}_{\mathit{x}})-({\mathit{a}}_{\mathit{y}}+{\mathit{b}}_{\mathit{y}})=-2{\mathit{s}}_{\mathit{y}}$$$$continuing,wehave$$$${\mathit{c}}^2+{\mathit{d}}^2={\mathit{a}}^2+{\mathit{b}}^2+4{\mathit{s}}_{\mathit{y}}^2$$$$+2{\mathit{s}}_{\mathit{y}}(-2{\mathit{s}}_{\mathit{y}})$$$$or{\mathit{c}}^2+{\mathit{d}}^2={\mathit{a}}^2+{\mathit{b}}^2.$$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 12/Jun/17

$$excellent!mrAjcour.thankyouvery$$$$much.$$

Commented by ajfour last updated on 12/Jun/17

$$thankyousir,ishallyetlookfor$$$$ashorterway..$$

Answered by ajfour last updated on 12/Jun/17

Commented by ajfour last updated on 12/Jun/17

$${\overline{l}}_x+\overline{c}=\overline{a}+{\overline{s}}_1...1\left(i\right)$$$${\overline{l}}_y+\overline{b}=\overline{c}+{\overline{s}}_2.....1\left(ii\right)$$$${\overline{l}}_x+\overline{b}=\overline{d}+{\overline{s}}_1.....1\left(iii\right)$$$${\overline{l}}_y+\overline{d}=\overline{a}+{\overline{s}}_2.....1\left(iv\right)$$$${\overline{l}}_x.{\overline{l}}_y={\overline{s}}_1.{\overline{s}}_2=0$$$${\overline{l}}_x.{\overline{s}}_2=-ls\left(\sin \theta \right),{\overline{l}}_y.{\overline{s}}_1=ls\left(\sin \theta \right)$$$$subtractingthetoplefttwoeqns.$$$$\overline{c}-\overline{b}=\overline{a}-\overline{d}$$$$\Rightarrow \overline{c}+\overline{d}=\overline{a}+\overline{b}$$$$So$$$$(\overline{c}+\overline{d}).(\overline{c}+\overline{d})=(\overline{c}+\overline{d}).(\overline{a}+\overline{b})$$$$c^2+d^2+2\overline{c}.\overline{d}=(\overline{c}+\overline{d}).(\overline{a}+\overline{b})...\left(2\right)$$$$from\left(i\right):$$$$\overline{c}-\overline{a}={\overline{s}}_1-{\overline{l}}_{x}andfrom\left(iv\right)$$$$\overline{d}-\overline{a}={\overline{s}}_2-{\overline{l}}_y$$$$takingdotproduct,$$$$(\overline{c}-\overline{a}).(\overline{d}-\overline{a})=-{\overline{s}}_1.{\overline{l}}_y-{\overline{s}}_2.{\overline{l}}_x$$$$=-ls\left(\sin \theta \right)+ls\left(\sin \theta \right)=0..\left(3\right)$$$$rearranging\left(ii\right)and\left(iii\right):$$$$\overline{c}-\overline{b}={\overline{l}}_y-{\overline{s}}_2$$$$\overline{b}-\overline{d}={\overline{s}}_1-{\overline{l}}_x$$$$dotproductyields,$$$$(\overline{c}-\overline{b}).(\overline{b}-\overline{d})={\overline{s}}_1.{\overline{l}}_y+{\overline{s}}_2.{\overline{l}}_x$$$$=ls\left(\sin \theta \right)-ls\left(\sin \theta \right)=0...\left(4\right)$$$$subtracting\left(4\right)and\left(3\right):$$$$\overline{c}.\overline{d}-\overline{c}.\overline{a}-\overline{a}.\overline{d}+a^2$$$$-\overline{c}.\overline{b}+\overline{c}.\overline{d}+b^2-\overline{b}.\overline{d}=0$$$$or$$$$2\overline{c}.\overline{d}-(\overline{c}+\overline{d}).(\overline{a}+\overline{b})+a^2+b^2=0$$$$....\left(5\right)$$$$subtracting\left(5\right)from\left(2\right):$$$$(c^2+d^2)-(a^2+b^2)=0$$$$c^2+d^2=a^2+b^2.$$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 12/Jun/17

$$sonicedearmrAjfour.thisproofis$$$$verybeautiful.ilovethis.thanks.$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com