Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 15572 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 12/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 12/Jun/17

$$circle:ctangenttosemicircleAEBat:$$$$points:E\mathrm{\&}D.AD=a=12,DB=b=5.$$$$....................................................$$$$1)DE=x=?,AE=?$$$$2)showthat:\measuredangle AED={45}^{\bullet }.$$

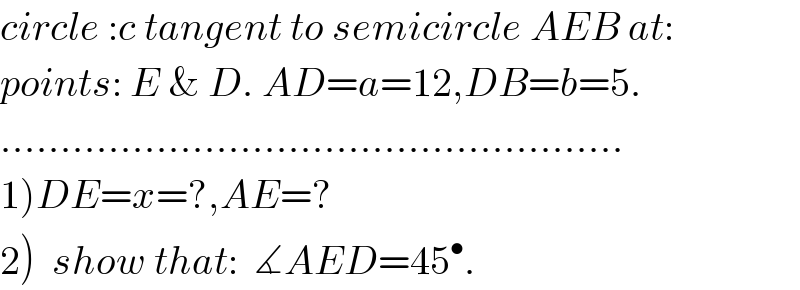
Answered by mrW1 last updated on 12/Jun/17

$$\mathrm{R}=\mathrm{radius}\mathrm{of}\mathrm{big}\mathrm{circle}$$$$\mathrm{r}=\mathrm{radius}\mathrm{of}\mathrm{small}\mathrm{circle}$$$$\mathrm{R}=\frac{\mathrm{a}+\mathrm{b}}{2}$$$$$$$$\mathrm{OD}=\mathrm{a}-\mathrm{R}=\frac{\mathrm{a}-\mathrm{b}}{2}$$$$\mathrm{OC}=\mathrm{OE}-\mathrm{CE}=\mathrm{R}-\mathrm{r}$$$${\mathrm{OC}}^2={\mathrm{OD}}^2+{\mathrm{DC}}^2$$$${(\mathrm{R}-\mathrm{r})}^2={\left(\frac{\mathrm{a}-\mathrm{b}}{2}\right)}^2+{\mathrm{r}}^2$$$$\mathrm{R}(\mathrm{R}-2\mathrm{r})=\frac{{(\mathrm{a}-\mathrm{b})}^2}{4}$$$$\Rightarrow \mathrm{r}=\frac{1}{2}[\mathrm{R}-\frac{{(\mathrm{a}-\mathrm{b})}^2}{4\mathrm{R}}]=\frac{{4\mathrm{R}}^2-{(\mathrm{a}-\mathrm{b})}^2}{8\mathrm{R}}$$$$=\frac{{(\mathrm{a}+\mathrm{b})}^2-{(\mathrm{a}-\mathrm{b})}^2}{4(\mathrm{a}+\mathrm{b})}=\frac{\mathrm{ab}}{\mathrm{a}+\mathrm{b}}$$$$$$$${\mathrm{x}}^2={2\mathrm{r}}^2-{2\mathrm{r}}^2\cos \mathrm{\angle }\mathrm{DOE}$$$$={2\mathrm{r}}^2+{2\mathrm{r}}^2\cos \mathrm{\angle }\mathrm{OCD}$$$$={2\mathrm{r}}^2(1+\frac{\mathrm{CD}}{\mathrm{OC}})={2\mathrm{r}}^2(1+\frac{\mathrm{r}}{\mathrm{R}-\mathrm{r}})$$$$={2\mathrm{r}}^2(1+\frac{1}{\frac{\mathrm{R}}{\mathrm{r}}-1})$$$$={2\mathrm{r}}^2(1+\frac{1}{\frac{{(\mathrm{a}+\mathrm{b})}^2}{2\mathrm{ab}}-1})$$$$=2{\left(\frac{\mathrm{ab}}{\mathrm{a}+\mathrm{b}}\right)}^2(1+\frac{2\mathrm{ab}}{{(\mathrm{a}+\mathrm{b})}^2-2\mathrm{ab}})$$$$=2{\left(\frac{\mathrm{ab}}{\mathrm{a}+\mathrm{b}}\right)}^2\left(\frac{{(\mathrm{a}+\mathrm{b})}^2}{{\mathrm{a}}^2+{\mathrm{b}}^2}\right)$$$$=\frac{2{\left(\mathrm{ab}\right)}^2}{{\mathrm{a}}^2+{\mathrm{b}}^2}$$$$\Rightarrow \mathrm{x}=\mathrm{ab}\sqrt{\frac{2}{{\mathrm{a}}^2+{\mathrm{b}}^2}}$$$$$$$${\mathrm{AE}}^2={\mathrm{y}}^2={2\mathrm{R}}^2-{2\mathrm{R}}^2\cos \mathrm{\angle }\mathrm{AOE}$$$$={2\mathrm{R}}^2(1+\cos \mathrm{\angle }\mathrm{EOB})$$$$={2\mathrm{R}}^2(1+\frac{\mathrm{OD}}{\mathrm{OC}})$$$$={2\mathrm{R}}^2(1+\frac{\mathrm{a}-\mathrm{b}}{2(\mathrm{R}-\mathrm{r})})$$$$\mathrm{R}-\mathrm{r}=\frac{\mathrm{a}+\mathrm{b}}{2}-\frac{\mathrm{ab}}{\mathrm{a}+\mathrm{b}}=\frac{{(\mathrm{a}+\mathrm{b})}^2-2\mathrm{ab}}{2(\mathrm{a}+\mathrm{b})}=\frac{{\mathrm{a}}^2+{\mathrm{b}}^2}{2(\mathrm{a}+\mathrm{b})}$$$${\mathrm{y}}^2={2\mathrm{R}}^2(1+\frac{{\mathrm{a}}^2-{\mathrm{b}}^2}{{\mathrm{a}}^2+{\mathrm{b}}^2})={2\mathrm{R}}^2\frac{{2\mathrm{a}}^2}{{\mathrm{a}}^2+{\mathrm{b}}^2}$$$$={(\mathrm{a}+\mathrm{b})}^2\frac{{\mathrm{a}}^2}{{\mathrm{a}}^2+{\mathrm{b}}^2}$$$$\mathrm{AE}=\mathrm{y}=\frac{\mathrm{a}(\mathrm{a}+\mathrm{b})}{\sqrt{{\mathrm{a}}^2+{\mathrm{b}}^2}}$$$$$$$${\mathrm{x}}^2+{\mathrm{y}}^2-2\mathrm{xycos}\mathrm{\angle }\mathrm{AED}={\mathrm{AD}}^2={\mathrm{a}}^2$$$$\frac{2{\left(\mathrm{ab}\right)}^2}{{\mathrm{a}}^2+{\mathrm{b}}^2}+\frac{{\mathrm{a}}^2{(\mathrm{a}+\mathrm{b})}^2}{{\mathrm{a}}^2+{\mathrm{b}}^2}-2\frac{\sqrt{2}\left(\mathrm{ab}\right)\mathrm{a}(\mathrm{a}+\mathrm{b})}{{\mathrm{a}}^2+{\mathrm{b}}^2}\cos \mathrm{\angle }\mathrm{AED}={\mathrm{a}}^2$$$${2\mathrm{b}}^2+{(\mathrm{a}+\mathrm{b})}^2-({\mathrm{a}}^2+{\mathrm{b}}^2)=2\sqrt{2}\mathrm{b}(\mathrm{a}+\mathrm{b})\cos \mathrm{\angle }\mathrm{AED}$$$$2\mathrm{b}(\mathrm{b}+\mathrm{a})=2\sqrt{2}\mathrm{b}(\mathrm{a}+\mathrm{b})\cos \mathrm{\angle }\mathrm{AED}$$$$1=\sqrt{2}\cos \mathrm{\angle }\mathrm{AED}$$$$\frac{1}{\sqrt{2}}=\cos \mathrm{\angle }\mathrm{AED}$$$$\Rightarrow \mathrm{\angle }\mathrm{AED}=\frac{\pi }{4}$$

Commented by mrW1 last updated on 12/Jun/17

$$\mathrm{you}\mathrm{are}\mathrm{right}\mathrm{sir},\mathrm{thanks}.\mathrm{I}\mathrm{have}\mathrm{fixed}.$$

Commented by mrW1 last updated on 12/Jun/17

$$\mathrm{you}\mathrm{are}\mathrm{welcome}\mathrm{sir}!\mathrm{thank}\mathrm{you}\mathrm{too}!$$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 12/Jun/17

$$thankyoudearmrW1.$$$$x=\frac{12\times 5}{12+5}\sqrt{2(1+\frac{2\times 12\times 5}{144-25})}=$$$$=\frac{60}{17}\sqrt{4.02}=7.07$$$$rightanswerforx:x=6.52$$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 12/Jun/17

$$cos\measuredangle OCD=\frac{CD}{OC}=\frac{r}{R-r}$$$$\Rightarrow x^2=2r^2(1+\frac{r}{R-r})=\frac{2{Rr}^2}{R-r}\Rightarrow x=r\sqrt{\frac{2R}{R-r}}$$$$r=\frac{ab}{a+b},R=\frac{a+b}{2}$$$$R-r=\frac{a+b}{2}-\frac{ab}{a+b}=\frac{a^2+b^2}{2(a+b)}$$$$\Rightarrow x=\frac{ab}{a+b}\sqrt{\frac{a+b}{\frac{a^2+b^2}{2(a+b)}}}=\frac{ab\sqrt{2}}{\sqrt{a^2+b^2}}$$$$y=\frac{a(a+b)}{\sqrt{a^2+b^2}}$$

Commented by mrW1 last updated on 12/Jun/17

$$\mathrm{you}\mathrm{are}\mathrm{right},\mathrm{thanks}.\mathrm{I}\mathrm{have}\mathrm{fixed}.$$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 12/Jun/17

$$thanksforyou.youranswerisvery$$$$beautiful.ilearnmanythingsfrom$$$$yourcommenetsandanswers.$$$$godblessyoumaster.$$

Answered by ajfour last updated on 12/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 12/Jun/17

$$thankyouverymuch.{it}^{\prime }sperfect!$$

Commented by ajfour last updated on 12/Jun/17

$$considering\mathrm{\Delta }COD:$$$$OD=\frac{(a+b)}{2}-b=\frac{a-b}{2}$$$$OE=R=\left(\frac{a+b}{2}\right)andCE=CD=r$$$$OC=OE-CE=R-r$$$${OD}^2={OC}^2-{CD}^2$$$$\Rightarrow {\left(\frac{a-b}{2}\right)}^2={(R-r)}^2-r^2$$$${\left(\frac{a-b}{2}\right)}^2=R^2-2rR$$$${\left(\frac{a-b}{2}\right)}^2={\left(\frac{a+b}{2}\right)}^2=2rR$$$$\Rightarrow 2rR=ab$$$$r=\frac{ab}{a+b}.$$$$\tan 2\theta =\frac{CD}{OD}=\frac{\left(\frac{ab}{a+b}\right)}{\left(\frac{a-b}{2}\right)}=\frac{2ab}{a^2-b^2}$$$$\frac{2\tan \theta }{1-\tan {}^2\theta }=\frac{2\left(b/a\right)}{1-{\left(b/a\right)}^2}$$$$\Rightarrow \tan \theta =\frac{b}{a}$$$$withCF\mathrm{\perp }DE$$$$\sin \mathrm{\angle }DCF=\frac{DF}{CD}=\frac{\left(x/2\right)}{r}$$$$\sin (\frac{\pi }{4}+\theta )=\frac{x}{2r}$$$$\frac{1}{\sqrt{2}}(\sin \theta +\cos \theta )=\frac{x}{2r}$$$$x=r\sqrt{2}(\frac{b}{\sqrt{a^2+b^2}}+\frac{a}{\sqrt{a^2+b^2}})$$$$x=\frac{\sqrt{2}ab}{(a+b)}\frac{(a+b)}{\sqrt{a^2+b^2}}$$$$x=\frac{\sqrt{2}ab}{\sqrt{a^2+b^2}}.$$$$y=2\left(AO\right)\cos \theta =2R\cos \theta$$$$asR=\frac{(a+b)}{2},wehave$$$$y=\frac{a(a+b)}{\sqrt{a^2+b^2}}andx=\frac{\sqrt{2}ab}{\sqrt{a^2+b^2}}$$$$fora=12,b=5$$$$y=\frac{204}{13}\approx 15.7and$$$$x=\frac{60\sqrt{2}}{13}\approx 6.526.$$$$\mathrm{\angle }AED=\mathrm{\angle }AEO+\mathrm{\angle }CEF$$$$=\theta +[\frac{\pi }{2}-(\frac{\pi }{4}+\theta )]$$$$=\frac{\pi }{4}.$$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 12/Jun/17

$$hidearmrAjfour!ihaveyourpicture$$$$buti{can}^{\prime }thearyoursound!{\left(ha\right)}^3$$$$whereisyoursolution?iamwaiting$$$$forit!$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com