Math Question and Answers


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 157695 by amin96 last updated on 26/Oct/21

	Answered by Rasheed.Sindhi last updated on 26/Oct/21

	$x^{16} + \frac{1}{x^{16}} = {(x^{8} + \frac{1}{x^{8}})}^{2} - 2 = 2207$ $x^{8} + \frac{1}{x^{8}} = \sqrt{2209} = 47$ $x^{8} + \frac{1}{x^{8}} = {(x^{4} + \frac{1}{x^{4}})}^{2} - 2 = 47$ $x^{4} + \frac{1}{x^{4}} = \sqrt{49} = 7$ $x^{4} + \frac{1}{x^{4}} = {(x^{2} + \frac{1}{x^{2}})}^{2} - 2 = 7$ $x^{2} + \frac{1}{x^{2}} = \sqrt{9} = 3$ $x^{2} + \frac{1}{x^{2}} = {(x + \frac{1}{x})}^{2} - 2 = 3$ $x + \frac{1}{x} = \sqrt{5}$ $. . . . . . .$ $. . . . .$
	Commented by amin96 last updated on 26/Oct/21

	I know this sir . how will it be after ?
	Commented by Rasheed.Sindhi last updated on 26/Oct/21
	Very hard to continue further sir.I have done only easy part. :)
	Answered by mr W last updated on 26/Oct/21

	${(x^{8} + \frac{1}{x^{8}})}^{2} = 2209 = 47^{2}$ $x^{8} + \frac{1}{x^{8}} = 47$ ${(x^{4} + \frac{1}{x^{4}})}^{2} = 49$ $x^{4} + \frac{1}{x^{4}} = 7$ ${(x^{2} + \frac{1}{x^{2}})}^{2} = 9$ $x^{2} + \frac{1}{x^{2}} = 3$ $l e t t = x^{2}$ $t + \frac{1}{t} = 3$ $t^{2} - 3 t + 1 = 0$ $p_{n} = t^{n} + \frac{1}{t^{n}} = x^{2 n} + \frac{1}{x^{2 n}}$ $p_{n + 1} = 3 p_{n} - p_{n - 1}$ $r^{2} - 3 r + 1 = 0$ $r_{1, 2} = \frac{3 \pm \sqrt{5}}{2}$ $p_{n} = r_{1}^{n} + r_{2}^{n} = {(\frac{3 + \sqrt{5}}{2})}^{n} + {(\frac{3 - \sqrt{5}}{2})}^{n}$ $a_{n} = {(x^{n} + \frac{1}{x^{n}})}^{2} = x^{2 n} + \frac{1}{x^{2 n}} + 2 = p_{n} + 2$ $\underset{n = 1}{\sum^{m = 2021}} a_{n} = \underset{n = 1}{\sum^{m}} (r_{1}^{n} + r_{2}^{n} + 2)$ $= \frac{r_{1} (r_{1}^{m} - 1)}{r_{1} - 1} + \frac{r_{2} (r_{2}^{m} - 1)}{r_{2} - 1} + 2 m$ $= \frac{(\frac{3 + \sqrt{5}}{2}) [{(\frac{3 + \sqrt{5}}{2})}^{m} - 1]}{\frac{3 + \sqrt{5}}{2} - 1} + \frac{(\frac{3 - \sqrt{5}}{2}) [{(\frac{3 - \sqrt{5}}{2})}^{m} - 1]}{\frac{3 - \sqrt{5}}{2} - 1} + 2 m$ $= \frac{(3 + \sqrt{5}) [{(\frac{3 + \sqrt{5}}{2})}^{m} - 1]}{\sqrt{5} + 1} - \frac{(3 - \sqrt{5}) [{(\frac{3 - \sqrt{5}}{2})}^{m} - 1]}{\sqrt{5} - 1} + 2 m$ $= (\frac{\sqrt{5} + 1}{2}) {(\frac{3 + \sqrt{5}}{2})}^{m} - (\frac{\sqrt{5} - 1}{2}) {(\frac{3 - \sqrt{5}}{2})}^{m} + 2 m - 1$
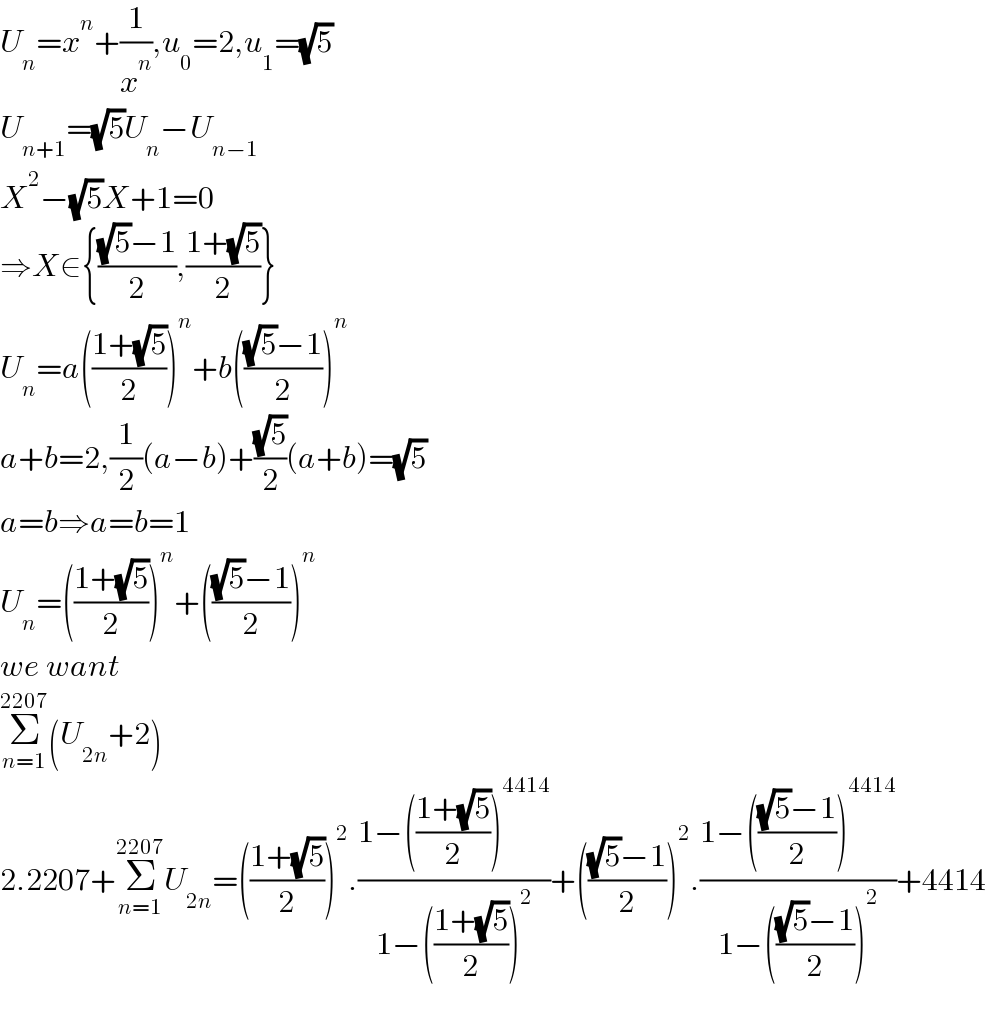
	Answered by mindispower last updated on 26/Oct/21
	$U_n =x^n +(1/x^n ),u_0 =2,u_1 =(√5) U_(n+1) =(√5)U_n −U_(n−1) X^2 −(√5)X+1=0 ⇒X∈{(((√5)−1)/2),((1+(√5))/2)} U_n =a(((1+(√5))/2))^n +b((((√5)−1)/2))^n a+b=2,(1/2)(a−b)+((√5)/2)(a+b)=(√5) a=b⇒a=b=1 U_n =(((1+(√5))/2))^n +((((√5)−1)/2))^n we want Σ_(n=1) ^(2207) (U_(2n) +2) 2.2207+Σ_(n=1) ^(2207) U_(2n) =(((1+(√5))/2))^2 .((1−(((1+(√5))/2))^(4414) )/(1−(((1+(√5))/2))^2 ))+((((√5)−1)/2))^2 .((1−((((√5)−1)/2))^(4414) )/(1−((((√5)−1)/2))^2 ))+4414$
	$U_{n} = x^{n} + \frac{1}{x^{n}}, u_{0} = 2, u_{1} = \sqrt{5}$ $U_{n + 1} = \sqrt{5} U_{n} - U_{n - 1}$ $X^{2} - \sqrt{5} X + 1 = 0$ $\Rightarrow X \in {\frac{\sqrt{5} - 1}{2}, \frac{1 + \sqrt{5}}{2}}$ $U_{n} = a {(\frac{1 + \sqrt{5}}{2})}^{n} + b {(\frac{\sqrt{5} - 1}{2})}^{n}$ $a + b = 2, \frac{1}{2} (a - b) + \frac{\sqrt{5}}{2} (a + b) = \sqrt{5}$ $a = b \Rightarrow a = b = 1$ $U_{n} = {(\frac{1 + \sqrt{5}}{2})}^{n} + {(\frac{\sqrt{5} - 1}{2})}^{n}$ $w e w a n t$ $\underset{n = 1}{\sum^{2207}} (U_{2 n} + 2)$ $2.2207 + \underset{n = 1}{\sum^{2207}} U_{2 n} = {(\frac{1 + \sqrt{5}}{2})}^{2} . \frac{1 - {(\frac{1 + \sqrt{5}}{2})}^{4414}}{1 - {(\frac{1 + \sqrt{5}}{2})}^{2}} + {(\frac{\sqrt{5} - 1}{2})}^{2} . \frac{1 - {(\frac{\sqrt{5} - 1}{2})}^{4414}}{1 - {(\frac{\sqrt{5} - 1}{2})}^{2}} + 4414$
	Answered by Raxreedoroid last updated on 28/Oct/21

	$x^{16} + \frac{1}{x^{16}} = {(x^{8} + \frac{1}{x^{8}})}^{2} - 2 = 2207$ $x^{8} + \frac{1}{x^{8}} = \sqrt{2209} = 47$ $x^{8} + \frac{1}{x^{8}} = {(x^{4} + \frac{1}{x^{4}})}^{2} - 2 = 47$ $x^{4} + \frac{1}{x^{4}} = \sqrt{49} = 7$ $x^{4} + \frac{1}{x^{4}} = {(x^{2} + \frac{1}{x^{2}})}^{2} - 2 = 7$ $x^{2} + \frac{1}{x^{2}} = \sqrt{9} = 3$ $x^{2} + \frac{1}{x^{2}} = {(x + \frac{1}{x})}^{2} - 2 = 3$ $x + \frac{1}{x} = \sqrt{5}$ $x^{2} - x \sqrt{5} + 1 = 0$ $x = \frac{\pm 1 + \sqrt{5}}{2} = φ^{\pm 1}$ $φ^{n} = φ^{n - 2} + φ^{n - 1}$ $φ^{n} = φ^{n + 2} - φ^{n + 1}$ $S = \underset{n = 1}{\sum^{2021}} {(φ^{n} + φ^{- n})}^{2}$ $S = \underset{n = 1}{\sum^{2021}} (φ^{2 n} + 2 + φ^{- 2 n})$ $S = \frac{(φ^{2}) ({(φ^{2})}^{2021} - 1)}{φ^{2} - 1} + 2 (2021) + \frac{(φ^{- 2}) ({(φ^{- 2})}^{2021} - 1)}{φ^{- 2} - 1}$ $S = \frac{(φ^{2}) ({(φ)}^{4042} - 1)}{φ} + 4042 - \frac{(φ^{- 2}) ({(φ)}^{- 4042} - 1)}{φ^{- 1}}$ $S = φ^{4043} + 4041 - {(φ^{- 1})}^{4043}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum